自注意力(Self-Attention)
认识CNN的局限性
输入与输出的局限性
CNN模型的输入向量的形状是固定的,其输出向量的形状也是固定的或可以根据不同的下游任务而唯一确定,即输入形状与下游任务共同确定了一个CNN模型的架构,具有较强的固定性。
在视觉中,输入大多为数字图像,其形状可以大致分为由尺寸和通道数来决定。
从输入图像的尺寸看,当CNN中没有全连接层时,本质上可以接受任意尺寸的输入,但这是狭隘的。若考虑其下游任务以及输出,如FCN(Fully Convolution Network),FCN通过最后通过反卷积将tensor还原到原始图像尺寸,即在CNN中,输入与输出(下游任务的要求)都影响着CNN网络的结构。
从通道数看,CNN本质上可以接受任意通道数的图像输入,但是其模型效果将会受到极大的影响。以一个使用通道数为3的数据集进行训练的CNN模型,但在测试阶段分别使用通道数为 1 和 6 的数据进行推理的情形为例,进行分析:
- 通道数为1的测试集:
- 情况: 如果使用通道数为 1 的数据进行推理,即灰度图像,而模型在训练时是使用 RGB 数据集训练的,模型可能会受到一些影响。
- 解释: 模型可能在训练时学到了关于颜色的特定信息,而在测试时,如果输入是灰度图像,那些颜色信息将不可用。
- 建议: 在这种情况下,模型可能会失去对颜色信息的敏感性,可能需要进行进一步的调整或微调,以适应灰度图像的特性。
- 通道数为6的测试集:
- 情况: 如果使用通道数为 6 的数据进行推理,模型可能会面临额外的挑战,因为它在训练时只见过 3 个通道的数据。
- 解释: 模型在训练时学到的权重是基于 3 个通道的数据的,对于额外的通道,模型可能无法有效利用这些信息。
- 建议: 对于通道数不匹配的情况,可以考虑进行通道的适当组合或调整。这可能包括降低通道数(例如,只使用前 3 个通道),或者通过某种方式将 6 个通道映射到 3 个通道,例如通过某种特定的数据预处理。
当模型的输入更复杂(sophisticated),是长度不定的向量序列(sequence)时,CNN不能很好地处理,且不能解决输出由输入和模型自行决定的下游任务,如生成类任务。
关联上下文信息的局限性
CNN中存�在局部连接和权值共享的归纳偏置:
- 局部连接:CNN使用卷积层通过滑动卷积核在输入上进行局部感受野的操作。每个神经元只与输入的一小部分区域相连,这意味着每个神经元只能接触到局部的上下文信息。
- 权值共享:共享的主要思想是,对于输入图像的不同位置使用相同的权重参数进行卷积操作。这意味着,无论卷积操作发生在图像的左上角、右下角,或者其他任何位置,都使用相同的卷积核进行权值计算。CNN的权值共享使得模型能够学习到图像中的局部特征,这也是一种对于上下文的假设。相邻位置上的权重共享使得模型能够对局部结构进行建模,这种权重共享使得CNN具有更强的归纳偏置。
在多通道卷积中,卷积核不同通道之间的权重参数是独立的。这使得网络能够学习不同通道之间的特征组合。这种设计有效地捕捉了输入数据中的多通道信息,提高了网络的表达能力。
CNN的设计理念认为:在图像任务中,局部结构通常更为重要,局部连接和权值共享使得CNN更适用于图像处理等任务。但也正是这种设计理念,使得CNN在面临长输入序列时不能很好地综合上下文信息、提取位置信息,因此Self-Attention应运而生,允许每个位置关注到序列中地所有其他位置。这种全局关联性质使得Transformer能够捕捉序列中的长距离依赖关系。
Self-Attention的原理
什么是Self-Attention
A self-attention module takes in inputs and returns outputs. What happens in this module? In layman’s terms, the self-attention mechanism allows the inputs to interact with each other (“self”) and find out who they should pay more attention to (“attention”). The outputs are aggregates of these interactions and attention scores.
Self-Attention接受任意向量数量的向量序列的输入,输出每一个向量所有向量(包括自身)的注意力分数。这使得Self-Attention在捕捉长距离依赖和处理序列中的全局关系时非常有效。
Self-Attention的核心思想
自注意力机制的核心思想是为序列中的每个向量分配一个权重(即注意力分数),该权重表示该元素与其他元素的关联强度。这个权重是通过计算输入序列中所有元素与当前元素之间的关系来确定的。通常,这个计算过程使用一个可学习的权重矩阵来完成,即用来生成Key,Query以及Value的权重矩阵。
Self-Attention的实现
定性分析详见文末。
注意考虑自注意力机制的实际意义,其输出是输入序列每个元素对每个位置的注意力分数。
因此,对于单头自注意力中的 Q、K 和 V 的维度 n_dim 通常等于输入序列的词嵌入维度 d_model。
对于多�头自注意力机制而言,n_dim 通常等于 d_model // num_heads,即词嵌入维度除以多头自注意力的头数。
定义输入
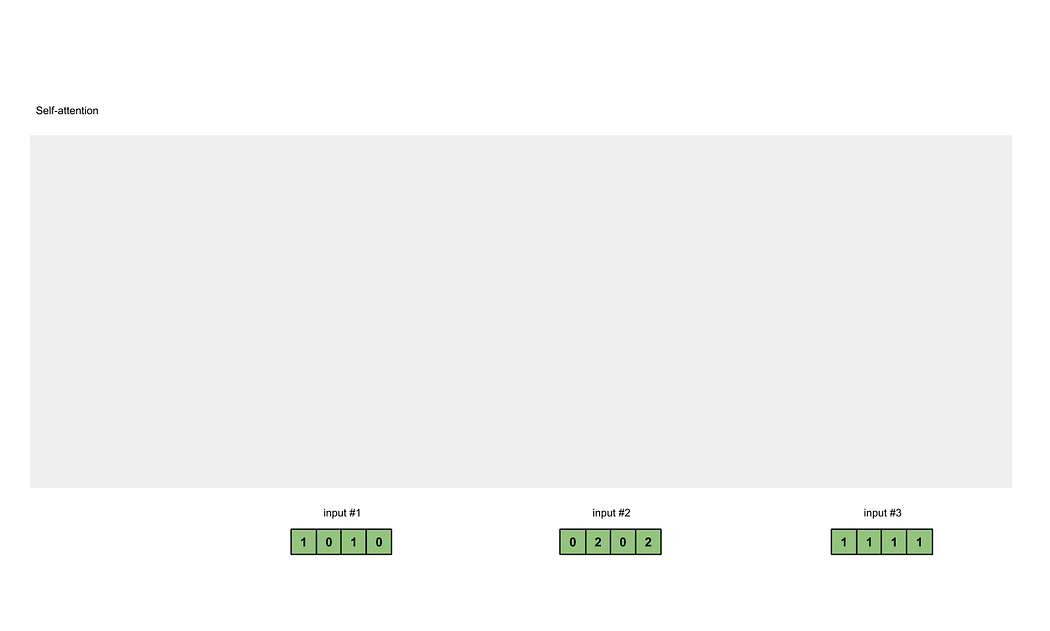
Self-Attention的输入是向量序列,其向量数量是任意的,计算每个输入向量之间的注意力分数。在本例中输入向量个数为3,同时为了统一性分析,计输入向量个数为个。
# define the input, which has a shape of (3, 4)
inputs = [[1, 0, 1, 0], [0, 2, 0, 2], [1, 1, 1, 1]]
inputs = torch.tensor(inputs, dtype=torch.float32)
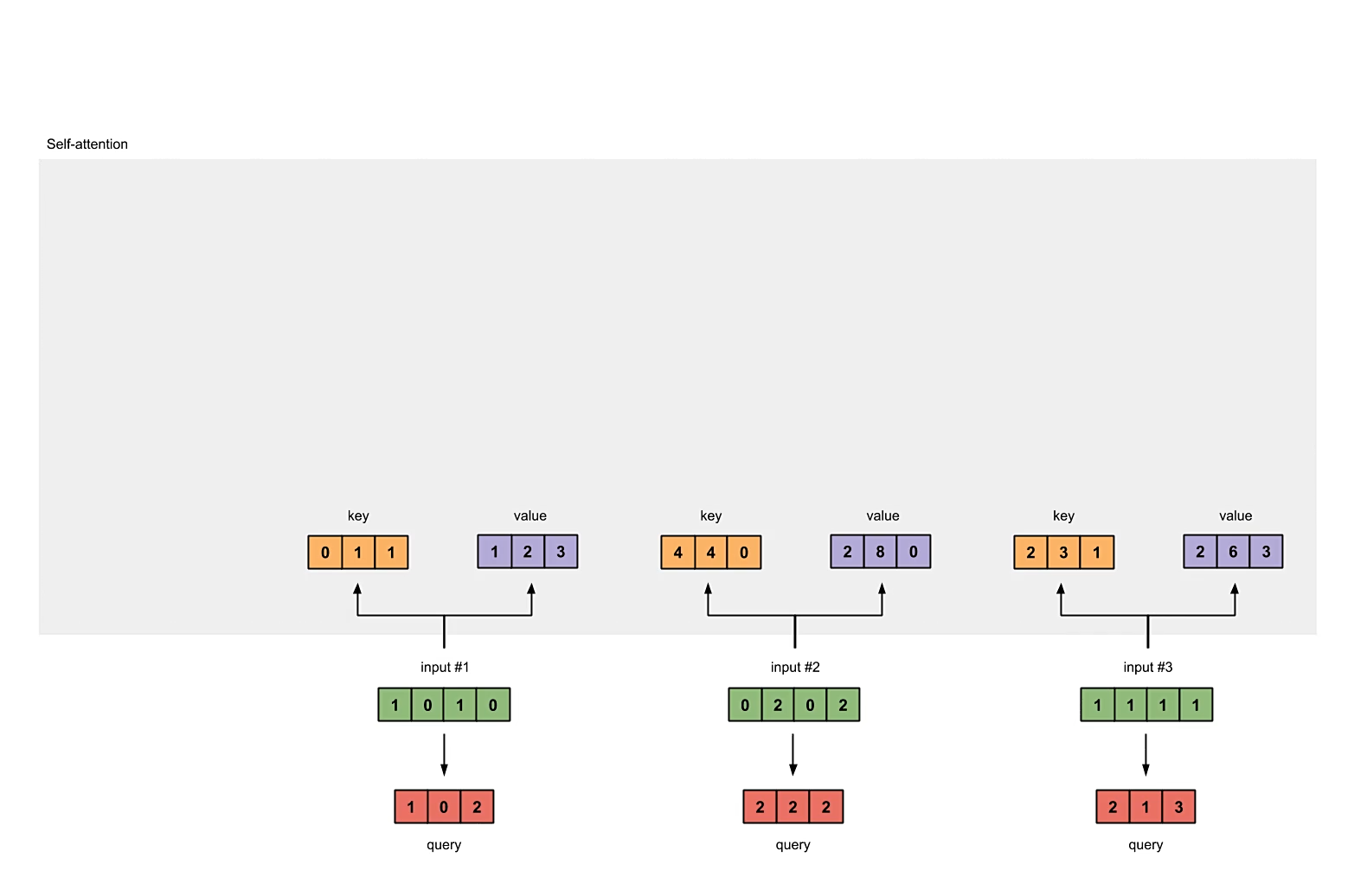
初始化权重矩阵
每个输入向量都会与3个权重向量做乘法得到3个新的向量,分别为key,query以及value。在本例中将新的向量维度设为3,由于输出的k、q、v矩阵大小均为,因此每个权重矩阵的形状应该是。为了统一性分析,计key,query以及value各向量维度为。
In a neural network setting, these weights are usually small numbers, initialised randomly using an appropriate random distribution like Gaussian, Xavier and Kaiming distributions. This initialisation is done once before training.
在实际应用中,权重通常是较小的数字,通过适当的随机分布(比如高斯、Xavier和Kaiming分布)进行随机初始化。
# define the weights for keys, queries and values
w_key = torch.tensor([[0, 0, 1], [1, 1, 0], [0, 1, 0], [1, 1, 0]], dtype=torch.float32)
w_query = torch.tensor([[1, 0, 1], [1, 0, 0], [0, 0, 1], [0, 1, 1]], dtype=torch.float32)
w_value = torch.tensor([[0, 2, 0], [0, 3, 0], [1, 0, 3], [1, 1, 0]], dtype=torch.float32)
计算key,query以及value
# compute keys, queries and values
keys = inputs @ w_key
queries = inputs @ w_query
values = inputs @ w_value
print("keys:\n", keys) # (3, 3)
print("queries:\n", queries) # (3, 3)
print("values:\n", values) # (3, 3)
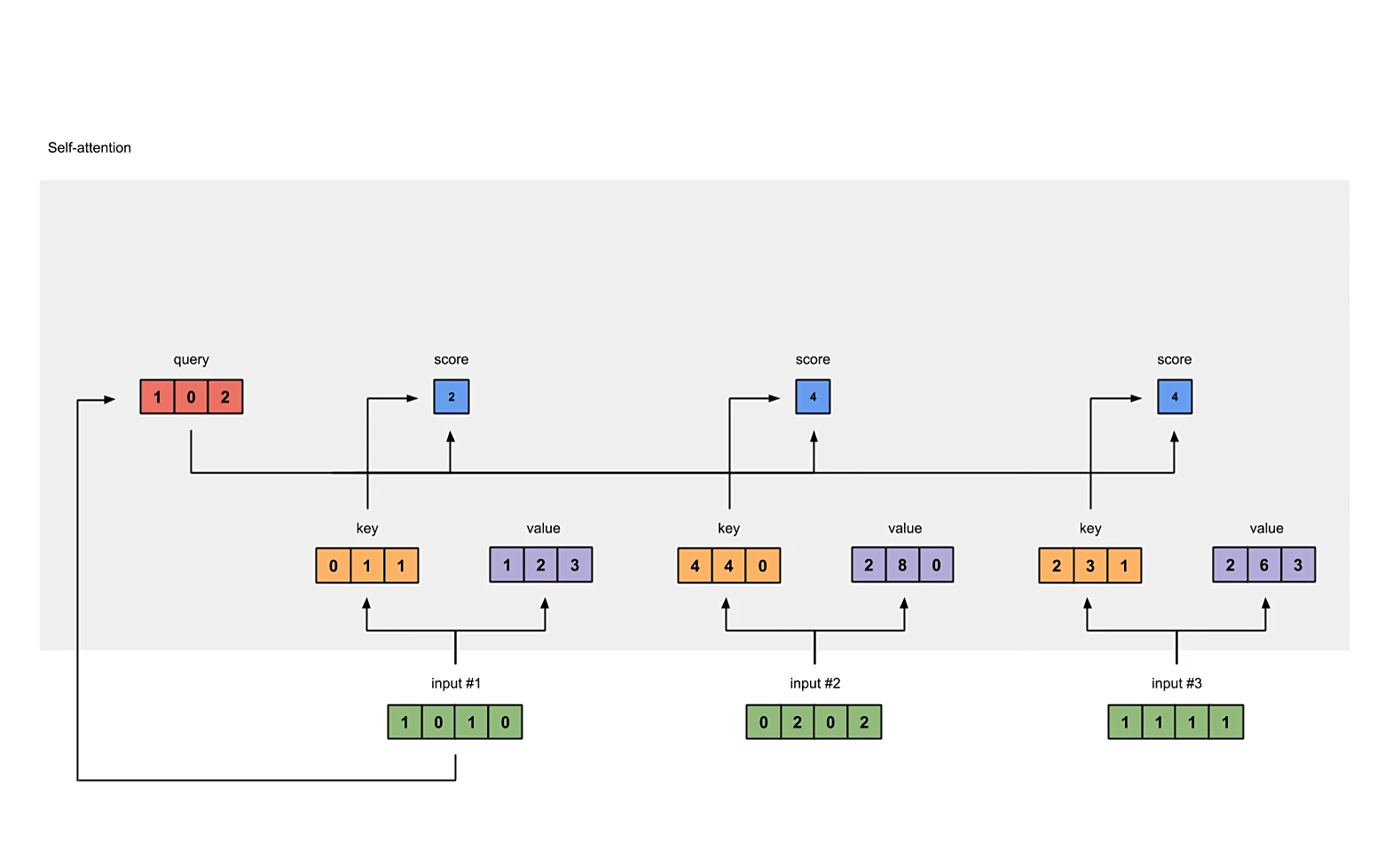
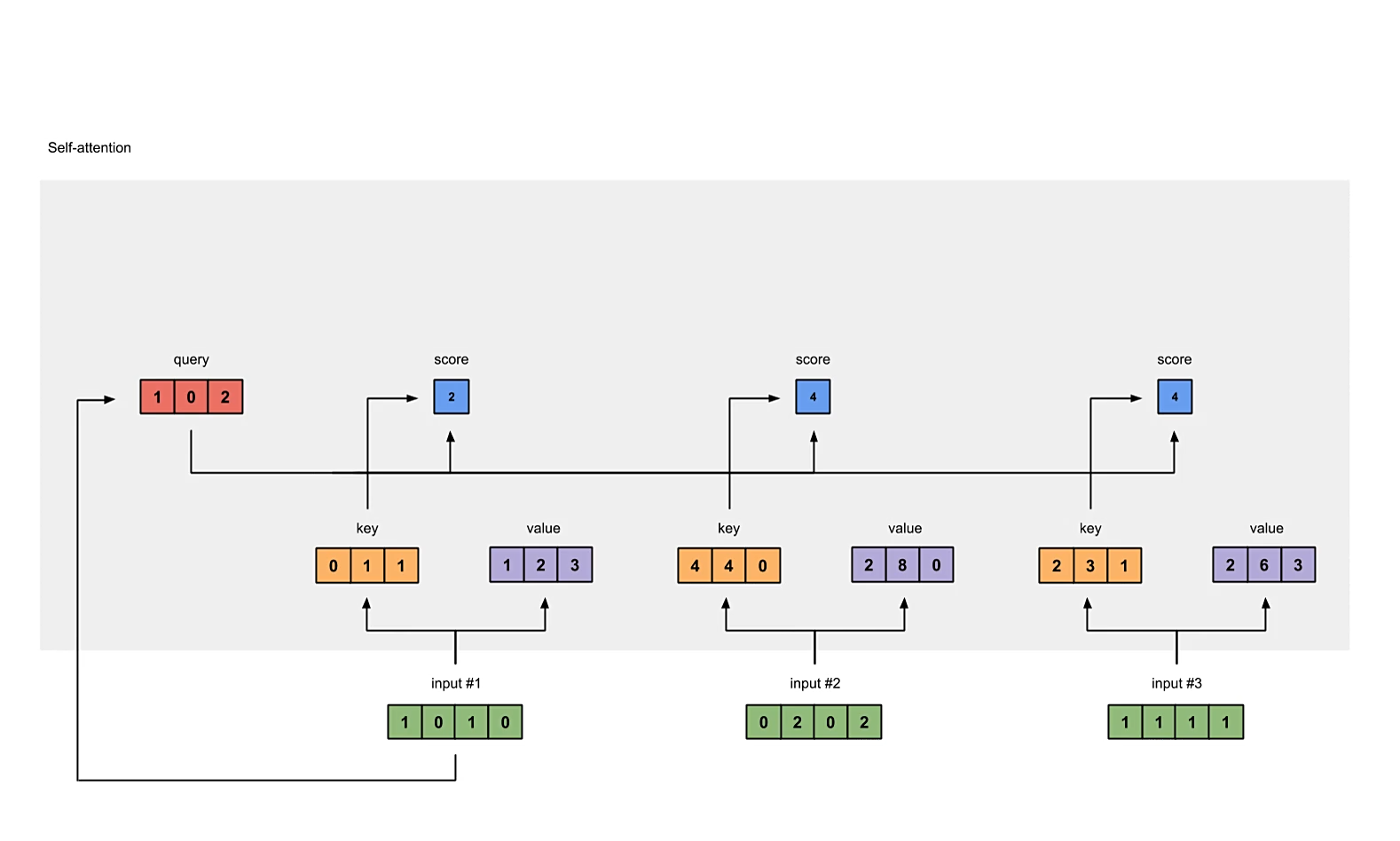
计算原始的注意力分数
我们要为每一个输入向量计算它对所有向量的注意力分数,包括对自身的。
原始注意力分数的计算方式为,使用自身的query分别与所有向量的key做内积(dot product),得到的scalar数量与输入向量个数相同,都为,即scores矩阵的形状应为。
# compute raw self-attention scores
scores = queries @ keys.T
print("attention scores:\n", scores)
注意,代码中提供的是计算所有向量的注意力分数,而图中演示的只是计算input #1的注意力分数。
对每一个向量计算出的注意力分数做softmax
# normalize the attention score
score_softmax = F.softmax(scores, dim=-1) # select the highest dimension
print("attention scores after normalization:\n", score_softmax)
将注意力分数与对应的value相乘
每一个输入向量对所有个向量计算得到的注意力分数,都要与其对应的value向量相乘,计算加权的注意力分数。最终的注意力分数矩阵的形状应为。
# compute the weighted values by doting score_softmax with values
# please be advised, this is dot product
weighted_values = values[:, None] * score_softmax.T[:, :, None]
print("weighted scores: \n", weighted_values)
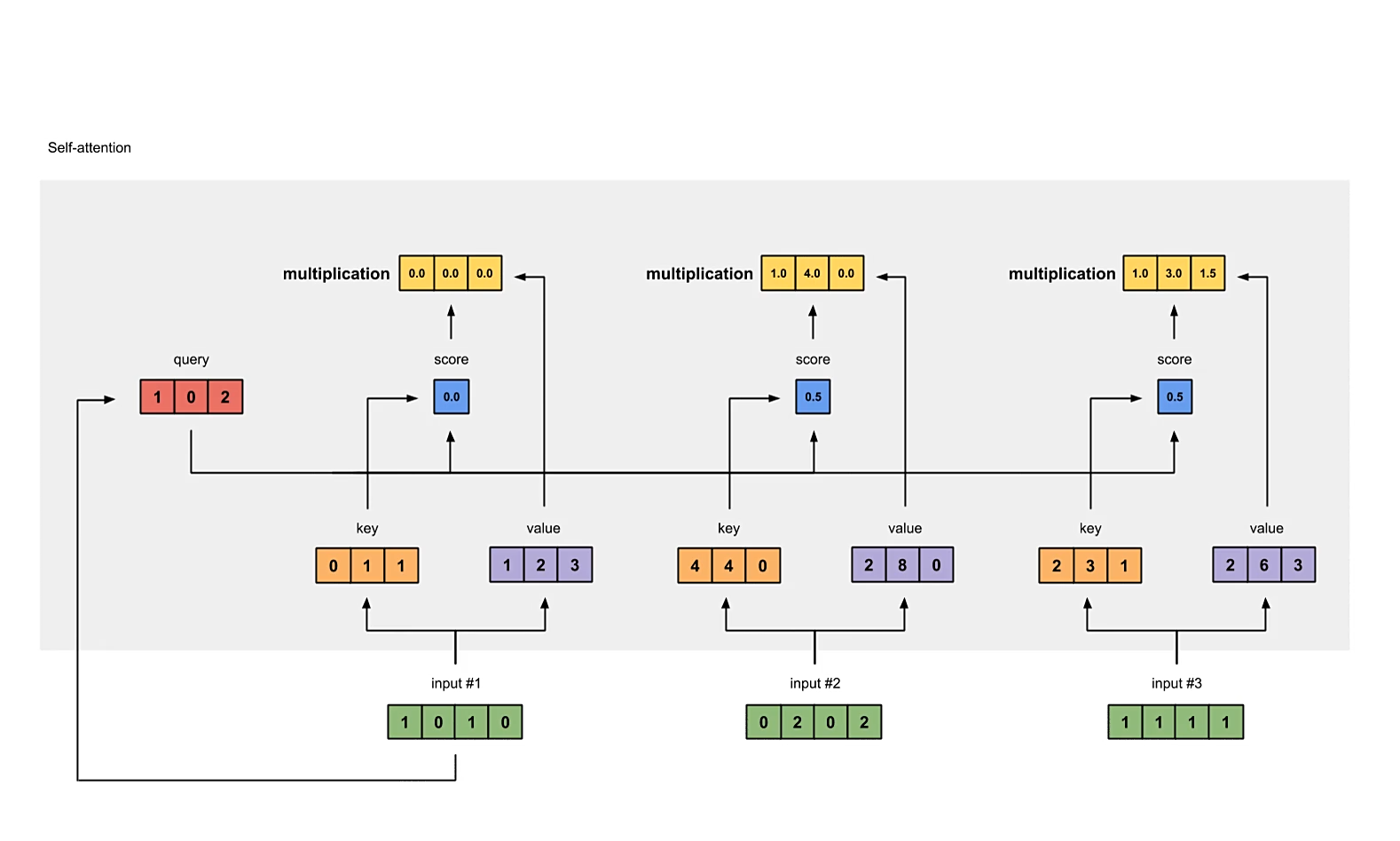
加权注意力分数求和
最后一步,对于每个向量得到的加权注意力分数进行求和,得到维度为的注意力分数向量,考虑到有个输入向量,因此最终的注意力分数矩阵的形状为。
根据推导,显然,最终Self-Attention的输出向量维度与value向量的维度相同,输出向量的数量与输入向量的数量相同。
# compute outputs
outputs = weighted_values.sum(dim=0)
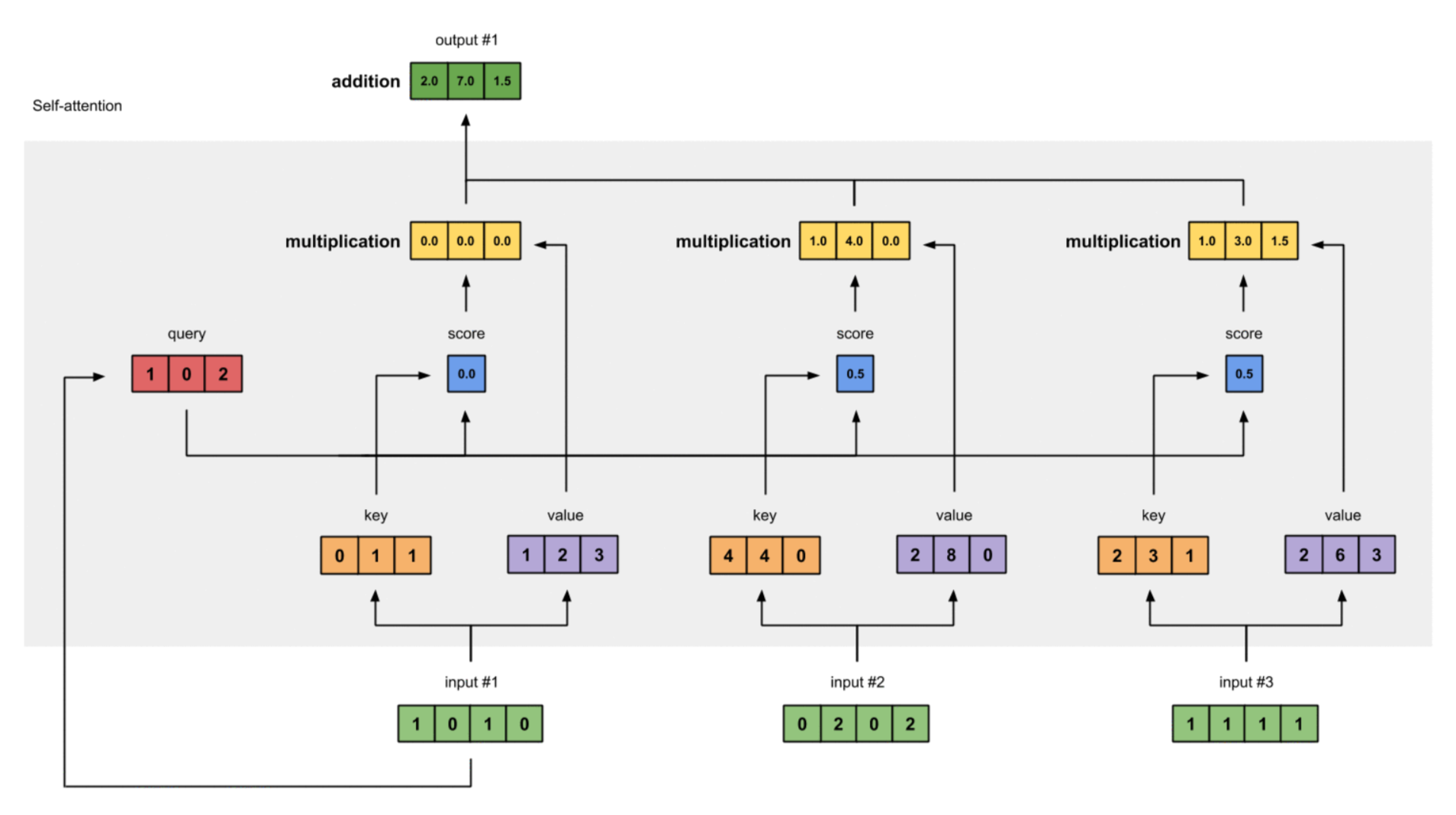
总结
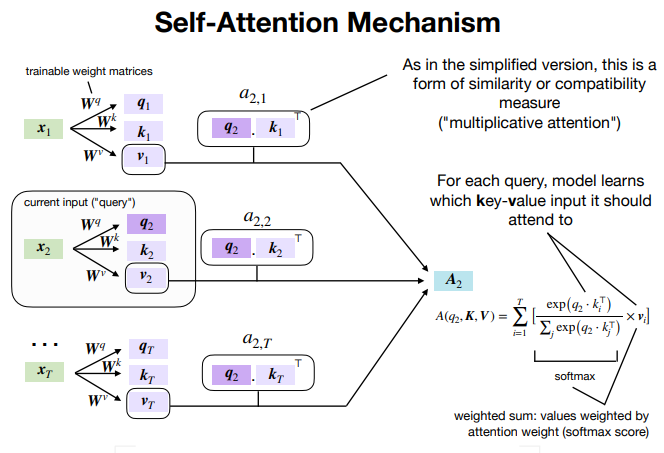
As mentioned in the above paragraph, we don’t only use dot product to find relevance. But we scale it as well by a factor of the square root of key dimension dk. This helps in making sure that the dot-products between query and key don’t grow too large for dk. If the dot product becomes too large then the softmax output will be very small. To avoid this, we scale the dot product.
在计算dot product后,为了避免点积运算经过softmax后的输出太小,在点积后除以key向量维度的平方根来进行缩放。
完�整代码
# simple code for Self-Attention
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plot
# define the input, which has the shape of (3, 4)
inputs = [[1, 0, 1, 0], [0, 2, 0, 2], [1, 1, 1, 1]]
inputs = torch.tensor(inputs, dtype=torch.float32)
# initialize the weights for keys, queries and values
w_key = torch.tensor([[0, 0, 1], [1, 1, 0], [0, 1, 0], [1, 1, 0]], dtype=torch.float32)
w_query = torch.tensor([[1, 0, 1], [1, 0, 0], [0, 0, 1], [0, 1, 1]], dtype=torch.float32)
w_value = torch.tensor([[0, 2, 0], [0, 3, 0], [1, 0, 3], [1, 1, 0]], dtype=torch.float32)
# compute keys, queries and values
keys = inputs @ w_key
queries = inputs @ w_query
values = inputs @ w_value
print("keys:\n", keys) # (3, 3)
print("queries:\n", queries) # (3, 3)
print("values:\n", values) # (3, 3)
# compute raw self-attention score
scores = queries @ keys.T
print("attention scores:\n", scores)
# normalize the attention score
score_softmax = F.softmax(scores, dim=-1) # select the highest dimension
print("attention scores after normalization:\n", score_softmax)
# compute the weighted values by doting score_softmax with values
# please be advised, this is dot product
weighted_values = values[:, None] * score_softmax.T[:, :, None]
print("weighted scores: \n", weighted_values)
# compute outputs
outputs = weighted_values.sum(dim=0)
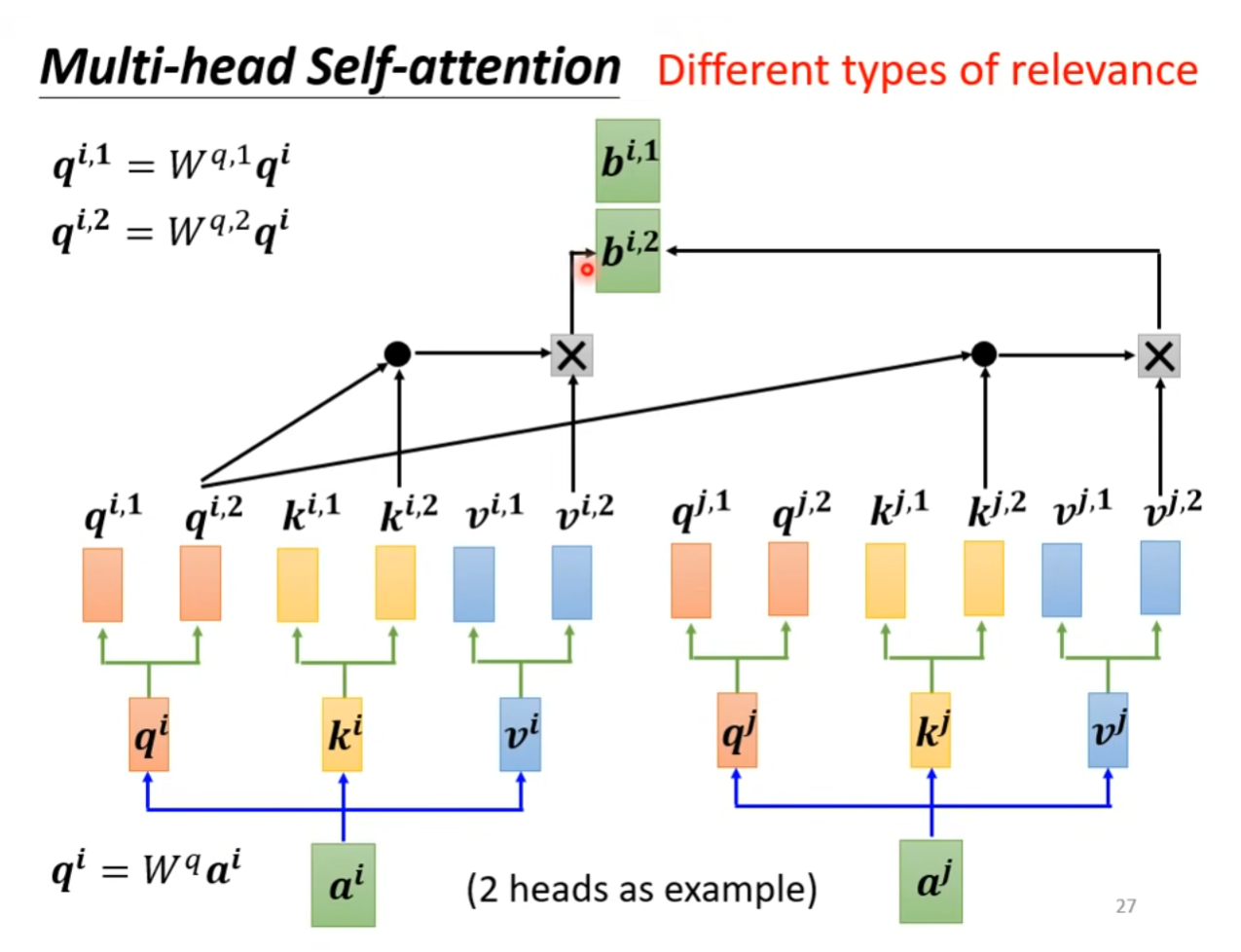
Multi-Head Self-Attention
多头自注意力机制是对自注意力机制的扩展,假设扩展成为 -head self-attention,则对每个输入向量生成对应的key,query和value后,再次使用个可学习的权重矩阵生成个不同的,以及。
在计算attention score时,使用每一个query查询对应的key,即只与其他每一个输入向量的做dot product。
Self-Attention与CNN的对比
Self-Attention可以看作是复杂化的CNN,CNN只能在感受野范围内考虑上下文信息,而Self-Attention可以自己学习感受野。

Self Attention 的计算
自注意力机制(Self-Attention Mechanism)是深度学习领域中的一种重要机制,尤其在处理序列数据和图像特征时展现出了强大能力。下面将以一个典型的自注意力机制为例,使用 Transformer 架构中的多头自注意力(Multi-Head Self-Attention)来说明其计算过程,以帮助理解其工作原理。假设我们的输入是一个序列,比如文本序列,其长度为 ,每个词向量的维度为 。
注意考虑自注意力机制的实际意义,其输出是输入序列每个元素对每个位置的注意力分数。
因此,对于单头自注意力中的 Q、K 和 V 的维度 n_dim 通常等于输入序列的词嵌入维度 d_model。
对于多头自注意力机制而言,n_dim 通常等于 d_model // num_heads,即词嵌入维度除以多头自注意力的头数。
输入形状
假设我们有一个文本序列,长度为 ,每个词表示为一个 维的向量。那么,整个输入的形状可以表示为 的矩阵。
自注意力机制的计算步骤
自注意力机制的核心思想是让序列中的每个元素(词向量)能够关注到序列中的其他元素,从而更好地理解它们之间的关系。具体来说,它通过计算三个向量——查询(Query,Q)、键(Key,K)和值(Value,V)来进行。
-
Query、Key、Value的生成:
- 首先,通过矩阵乘法,将输入的词向量矩阵分别与三个不同的权重矩阵相乘,生成 Q、K、V 三个矩阵。假设权重矩阵的维度均为 (其中 是查询和键的维度),那么 Q、K、V 的形状均为 。
-
计算注意力权重:
- 接下来,计算 Q 与 K 之间的相似度,通常使用点积(Dot Product)的方式,即每个查询向量 Q 与所有键向量 K 进行点积。点积的结果是一个 的矩阵,其中的每个元素表示查询向量与键向量之间的相似度。为了使这个矩阵中的元素处于同一尺度,通常会除以 ,以避免过大的点积值导致 softmax 函数饱和。
- 然后,对上述得到的矩阵应用 softmax 函数,得到注意力权重矩阵。这个矩阵的每一行都是一个概率分布,表示序列中每个元素对其他元素的注意力权重。
-
加权求和:
- 最后,将注意力权重矩阵与值矩阵 V 进行矩阵乘法,得到最终的注意力输出。这个过程可以视为对 V 矩阵中的每个值向量进行加权求和,权重由注意力权重矩阵决定。
多头自注意力
在实际应用中,往往采用多头自注意力(Multi-Head Attention)来增强模型的表示能力。具体来说,就是将上述过程重复多次,每次使用不同的权重矩阵来生成 Q、K、V,然后将多次得到的注意力输出进行拼接或平均,形成最终的多头注意力输出。
示例
假设输入的文本序列长度为 ,每个词向量的维度为 ,(查询和键的维度)。那么,Q、K、V 的形状均为 。在计算注意力权重时,得到的矩阵形状为 。最后的注意力输出形状同样为 (如果是多头自注意力,则可能需要将多个头的输出拼接或平均,具体形状取决于头的数量和后续处理方式)。
自注意力机制通过让序列中的每个元素都能“看到”其他元素,并根据它们之间的关系调整自己的表示,从而增强了模型对序列数据的理解能力,这对于处理自然语言处理任务(如翻译、文本生成等)和图像特征提取(如在视觉 Transformer 中)等场景都有着重要作用。
自注意力中的掩码 Mask
自注意力中有多种掩码类型,但实现方式大致相同,其作用大概可以分为一下几种。
- 防止注意力机制关注填充(padding)标记
- 实现因果注意力(causal attention),即每个位置只能关注它自己和之前的位置,常用于 Decoder 中
- 在特定任务中屏蔽某些不相关的输入