Understanding Diffusion Models: A Unified Perspective
简介 Introduction
作者认为,生成模型可以分为三大类:
- GAN:通过对抗的方式进行学习
- likelihood-based:学习一个使得当前数据集出现概率最高的模型,包括 autoregressive models,normalizing flows 和 VAEs 等等
- energy-based:将分布学习为任意灵活的能量函数,然后归一化。score-based 和 energy-based 很相似,学习的是 energy-based model 的 score。
本文重点讨论的 Diffusion Model,既可以用 likelihood-based 的观点来解释,也可以使用 score-based 的观点来解释。
背景 Background
地穴寓言(Allegory of the Cave)讲的是一群人一生都被锁在洞穴里,只能看到投射到他们面前墙壁上的二维阴影,这些阴影是由看不见的三维物体在大火前经过而产生的。对这样的人来说,他们所观察到的一切实际上都是由他们永远看不到的高维抽象概念所决定的。

作者从地穴寓言(Allegory of the Cave)中引出 VAE 和 DM 的直观思想,即观测到的数据 是由隐变量 生成的,通过观测到的数据来估计隐变量的分布,就可以通过采样隐变量来生成数据。
证据下界 Evidence Lower Bound
作者首先从似然模型的角度引出证据下界(ELBO)。

直接最大化似然存在对于如自然图像生成等复杂的自然情况是不现实的,因此引入证据下界:证据在这里即是观测数据的似然,下界代表 ELBO 是似然的下界,即:
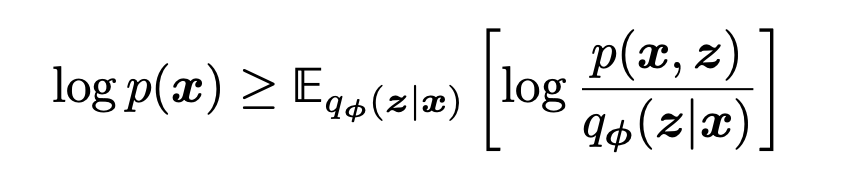
其中, 是变分分布(variational distribution),即带有参数的模型,根据观测值来预测隐变量,类似于 VAE 中的编码器 Encoder,通过优化参数来逼近隐变量的真实分布 。
作者给出了 ELBO 的两种证明方式,分别为使用 Jensen's Inequlity,以及通过引入 KL 散度。
Jensen's Inequlity:
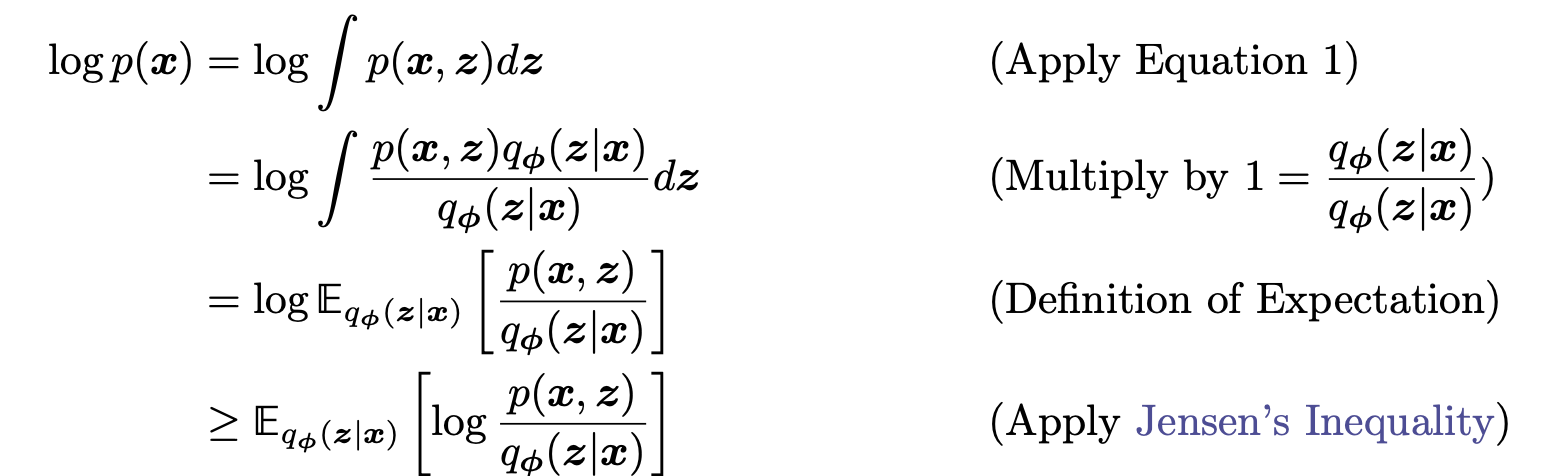
引入 KL 散度:通过引入 KL 散度,可以更直观的体现证据下界的由来,由于 KL 散度适中大于等于 0,因此

变分自编码器 Variational Autoencoders
进一步对 ELBO 的公式进行推导:
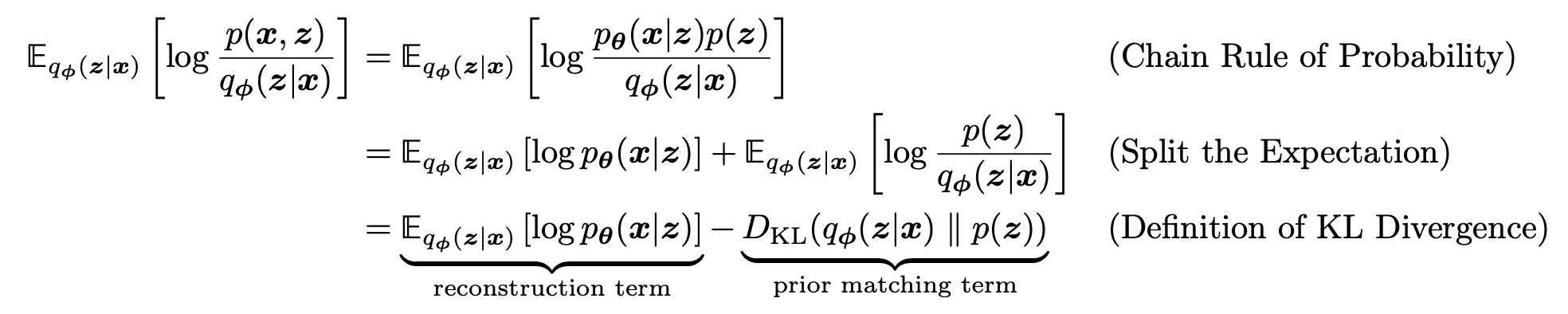
引入 VAE 的解码器 Decoder ,将隐变量映射为数据空间的可观测数据,带有可训练的参数 。
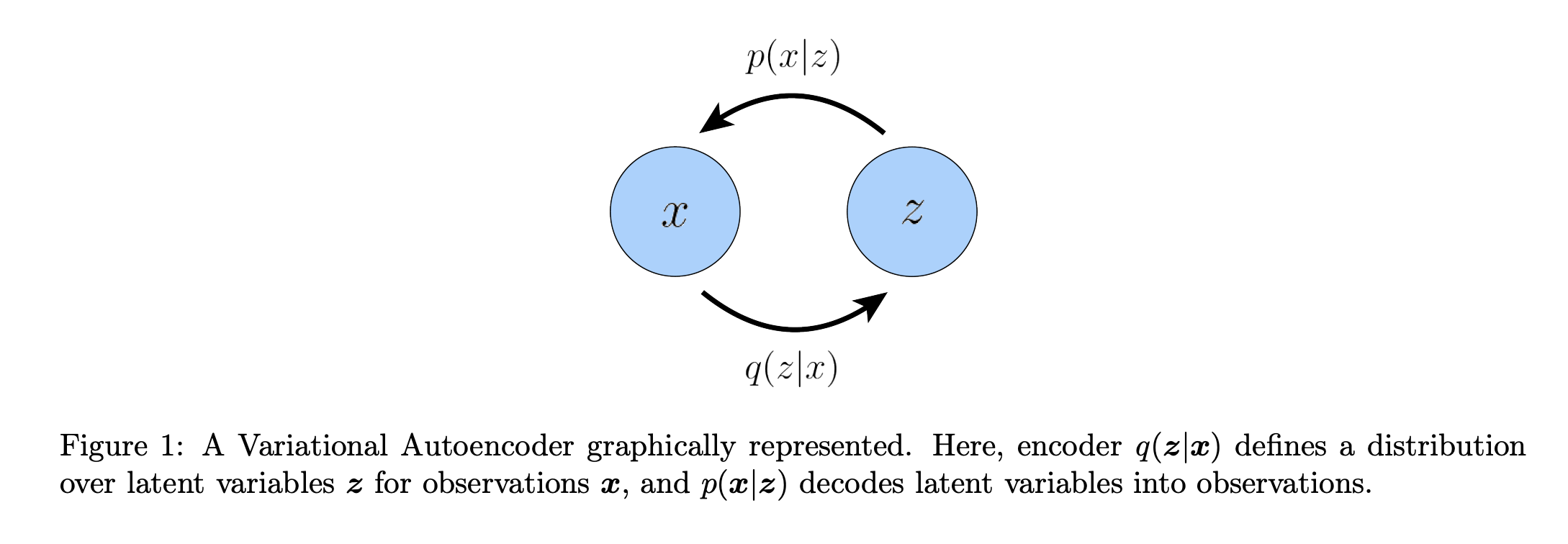
变分自编码器可以分为两部分:
- 变分:引入了变分分布,即 Encoder 项,预测真实的隐变量分布,在上述 ELBO 推导中体现为 prior matching term。
- 自编码器:VAE 将数据空间的可观测数据映射到隐空间,再从隐空间中恢复出来,在上述 ELBO 推导中可以体现为 reconstruction term。
重参数化技巧
VAE 的 Encoder 通常被设计为对角方差的多元高斯,所谓对角方差,就是没有协方差的意思。
与其对应的先验 Prior 为标准的多元高斯,
下界的 KL 散度项即 prior matching term 是可以算出解析解的,而前一项即 reconstruction term 则通过蒙特卡洛估计得到,也就是连续离散,使用有限的数据集来估计期望 。
我们的目标函数可以写成
其中, 是从 中采样得到的,每个 都是通过随机高斯分布采样的过程得到的,无法进行求导。
为了解决这个问题,引入重参数化技巧,重参化的精妙之处在于使用标准的随机过��程构造任意随机过程, 学习只学习构造的参数, 而随机过程是不参与梯度计算的。
假设随机过程为 ,则可以写作:
在 VAE 当中, 任意一次从 中对 的采样可以表示为:
其中, 表示 element-wise 的乘积。
VAE 就是借助与重参化的技巧和蒙特卡洛估计来同时更新 和 的。训练完成后,只需要在 上进行采样, 输入 decoder 就可以得到预测的结果了,encoder 已经不需要了。
的维度通常大大小于 ,这样可以迫使模型学习最有用的特征表示。
多层变分自编码器 Hierachical Variational Autoencoders
在 VAE 的基础上嵌套多层 VAE,增加更深层的隐变量即得到了多层变分自编码器 HVAE。
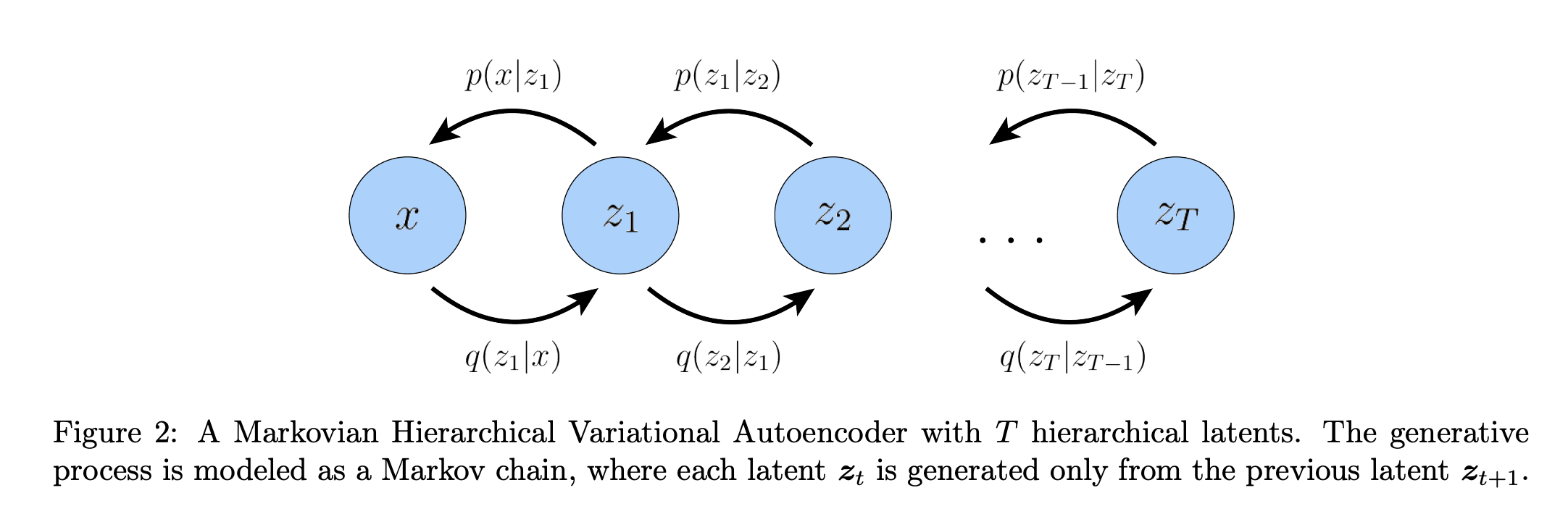
一般情况下,HVAE 中的每一层隐变量 是由其之前的所有隐变量决定的,不过本文只针对马尔可夫过程的 HVAE,也就是仅由 决定,这也被称为 MHVAE。

变分扩散模型 Variational Diffusion Models
一种理解 VDM 最简单的思路,就是将 VDM 看成 MHVAE,同时需要满足三个额外的限制:
- 隐变量的维度需要和输入图片维度一致
- Encoder 的每一步 encode 并不是学习得到的,而是实现设计好的高斯分布的融合。换句话说,每一步是以上一步为中心的高斯分布
- 每一步的高斯分布参数会发生一定的变化,使得最后一步接近标准高斯分布
其中,最重要的假设是第 2 条,去掉了 HVAE 中 Encoder 的参数 。
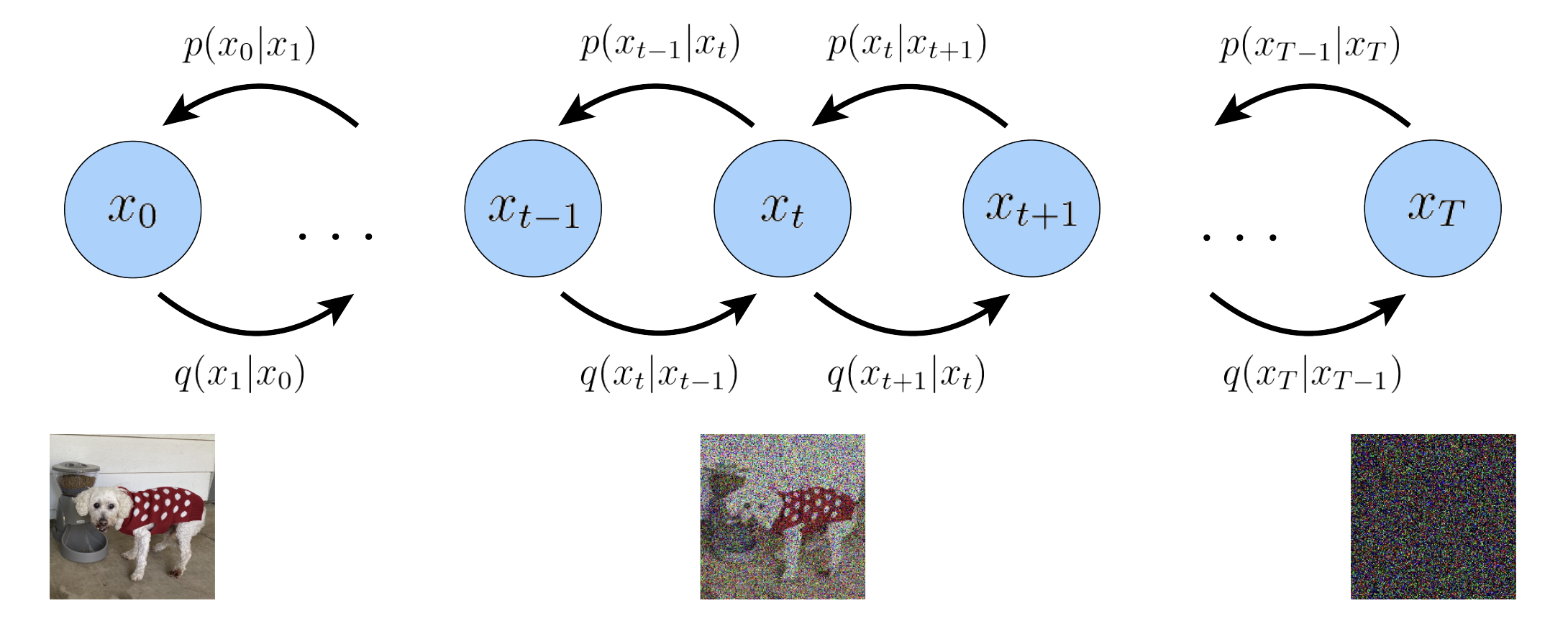
引入 Noise Schedule
根据第一点限制,模型不需要再区分隐变量 和数据空间的 了,统一使用 来表示任意时刻的数据即可。当 时, 指的是原始图片。当 时,表示对应步数的数据。
根据第二点限制,每一步的高斯参数人为设计为 ,其中 是一个潜在的可学习的参数,这里是个超参数,随着步数的变化而变化,即引入了 Noise Schedule。因此,有
根据第三点限制,最终的分布 是一个标准的高斯分布,其本质是真实分布逐渐变为标准高斯分布的过程。
其中, 。
将三个假设对应的数学表示带入 HVAE 的下界公式中,得到如下的新形式:
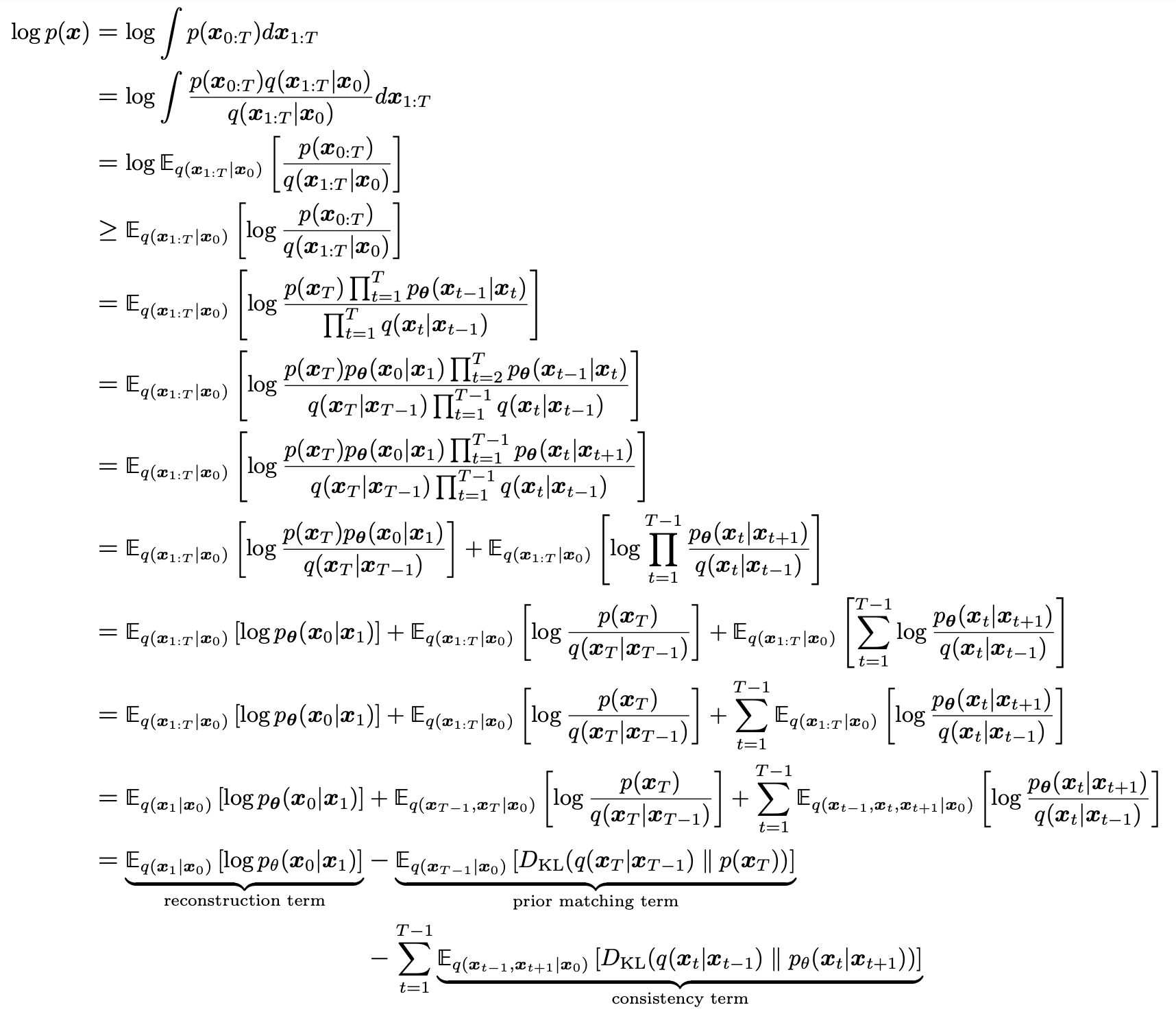
- reconstruction term:在原始 VAE 下界公式中也出现了,通过给定的第一步加噪版本来预测原始图像
- prior matching term:没有可训练的参数,当 T 步数足够大时,最终的分布是标准高斯分布,该项值为0
- consistency term:维持加噪与降噪的一致性,训练 VDM 的开销也主要来自该项,因为需要在每个时间步进行优化
但是通过蒙特卡罗方法进行优化并不是最优的选择,因为某些项中具有多个随机变量,通过蒙特卡罗方法计算多个随机变量的数学期望会导致方差过大,因此通过贝叶斯法则进行优化可以得到:

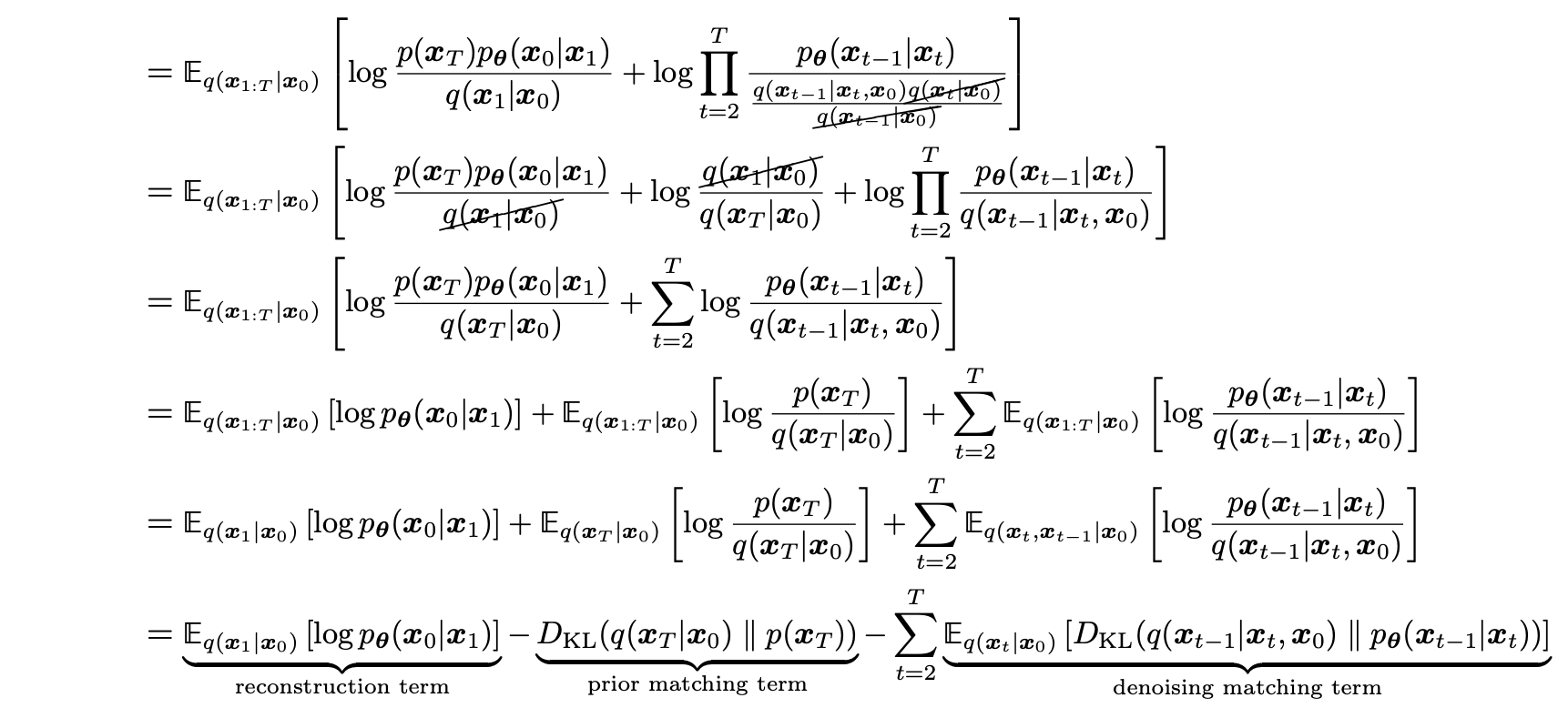
优化后 ELBO 的前两项没有发生本质的��变化,着重解释第三项 denoising matching term。
- reconstruction term:在原始 VAE 下界公式中也出现了,通过给定的第一步加噪版本来预测原始图像
- prior matching term:没有可训练的参数,当 T 步数足够大时,最终的分布是标准高斯分布,该项值为0
- denoising matching term:其中, 可以看作是待学习的降噪模型,而 可以看作是真实的降噪过程的标签,最大化 ELBO 即最小化 denosing matching term
确定的扩散过程
结合贝叶斯法则和重参数化技巧:
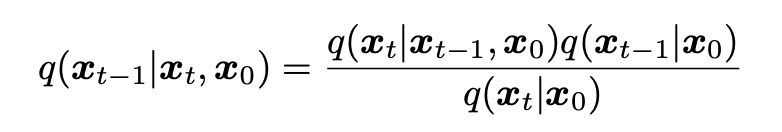
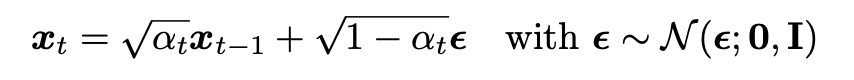
可以得到如下推导:
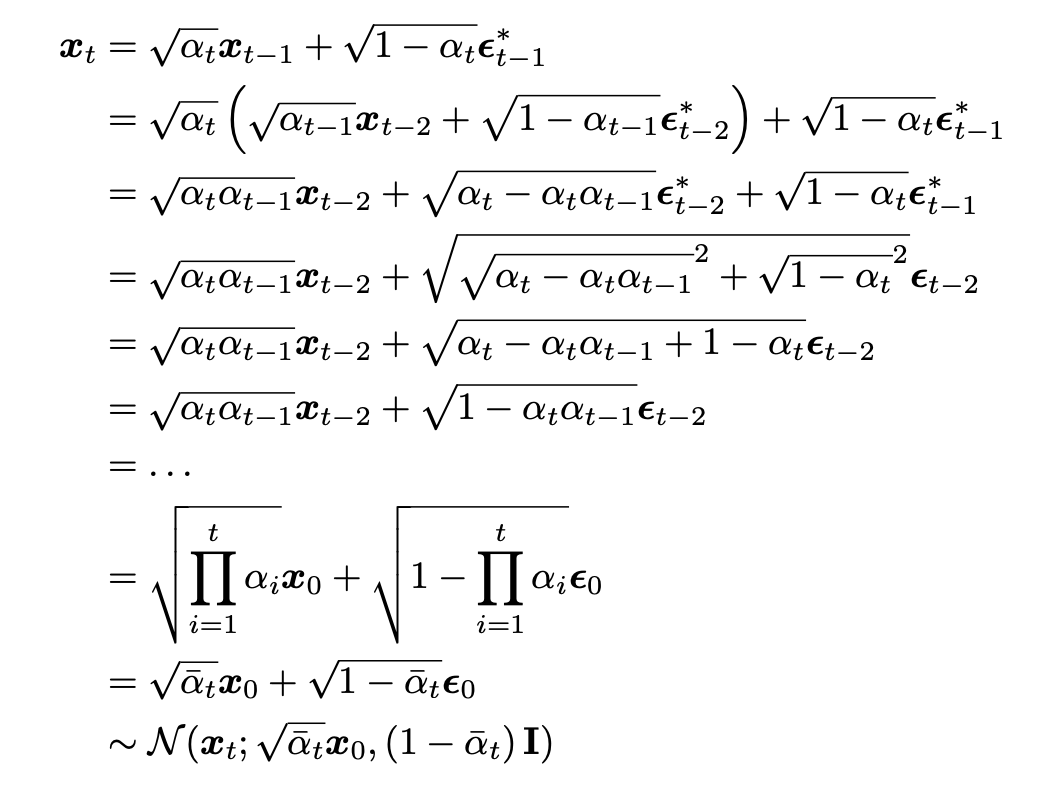
在这里,通过原始图像 和时间步的参数 ,我们可以直接获得任意时间步对应的原始图像加噪版本,换句话说,DM 的扩散过程是确定的,不需要根据时间步一步一步迭代得到相应的结果。
三种等价的解释
通过对 denoising matching term 进行不同侧重的进一步推导,可以得到对扩散模型的三种等价的解释。
-
训练扩散模型等价于训练一个模型来预测原始图片 :
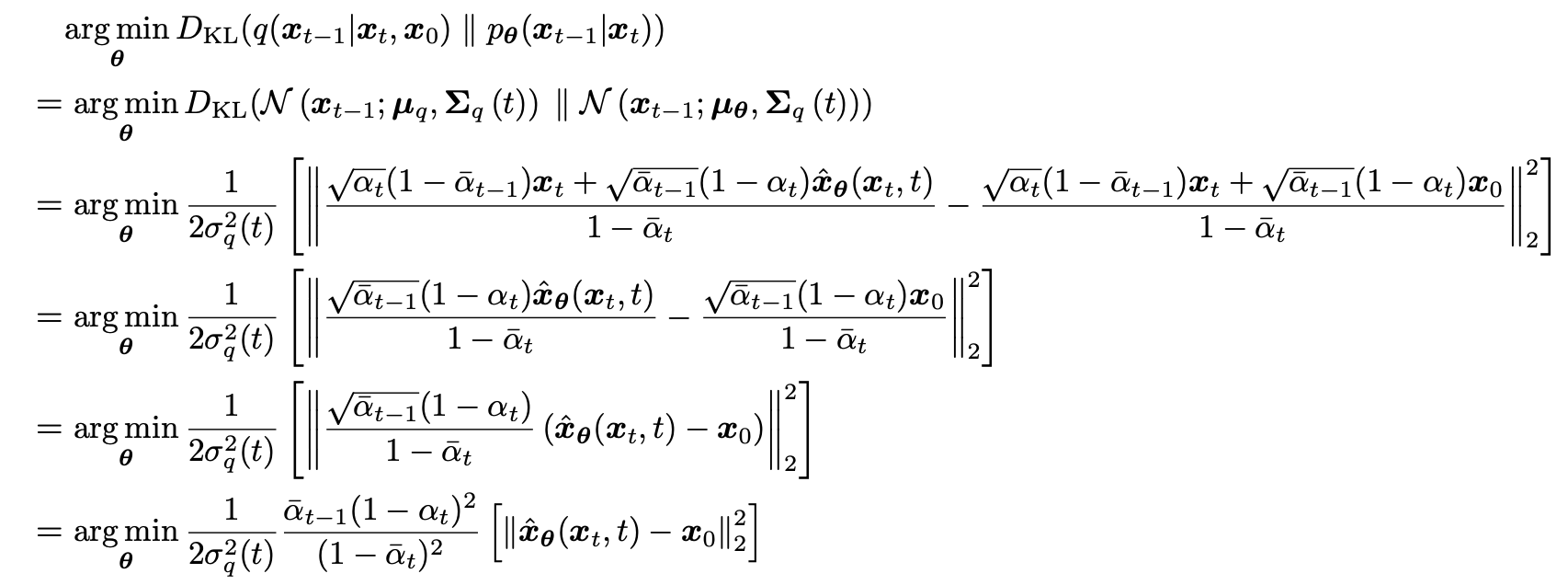
-
训练扩散模型等价于训练一个模型来预测初始噪声 :
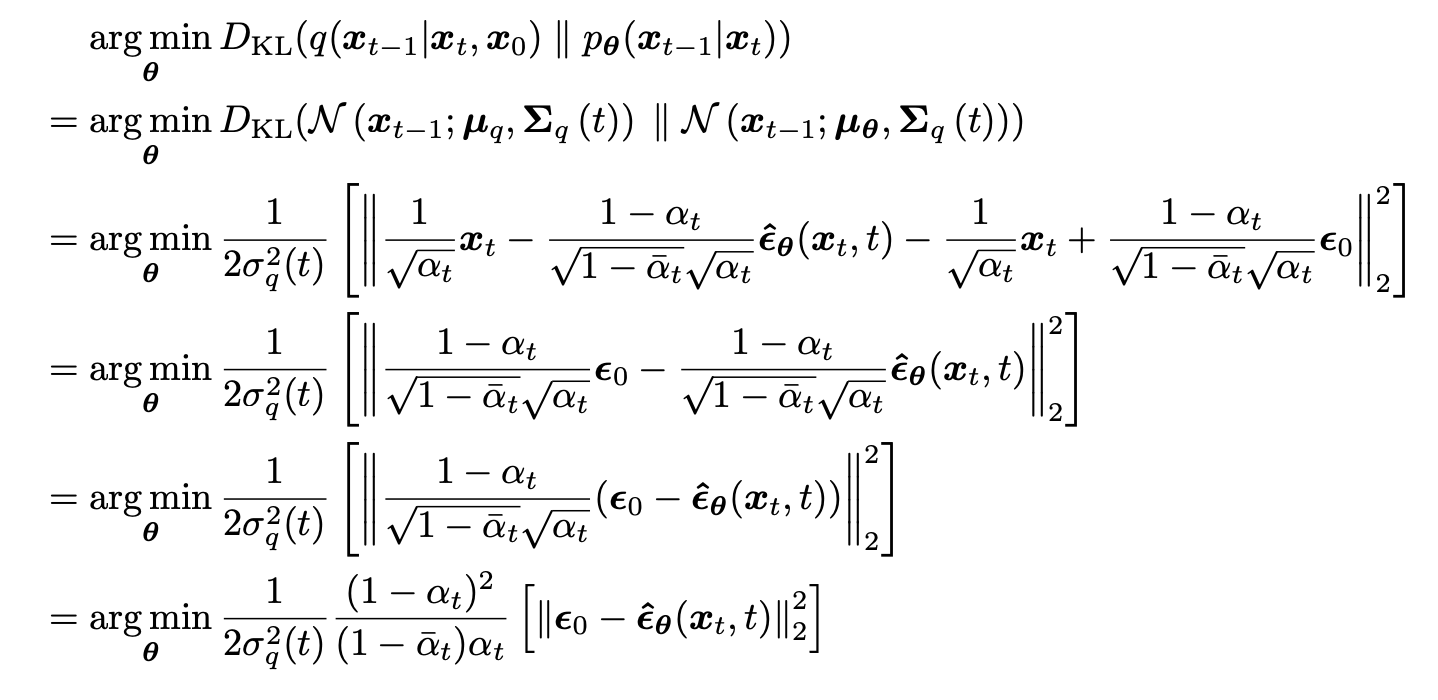
-
训练扩散模型等价于训练一个模型来预测 score function,即任意噪声等级下的图像的分数 :
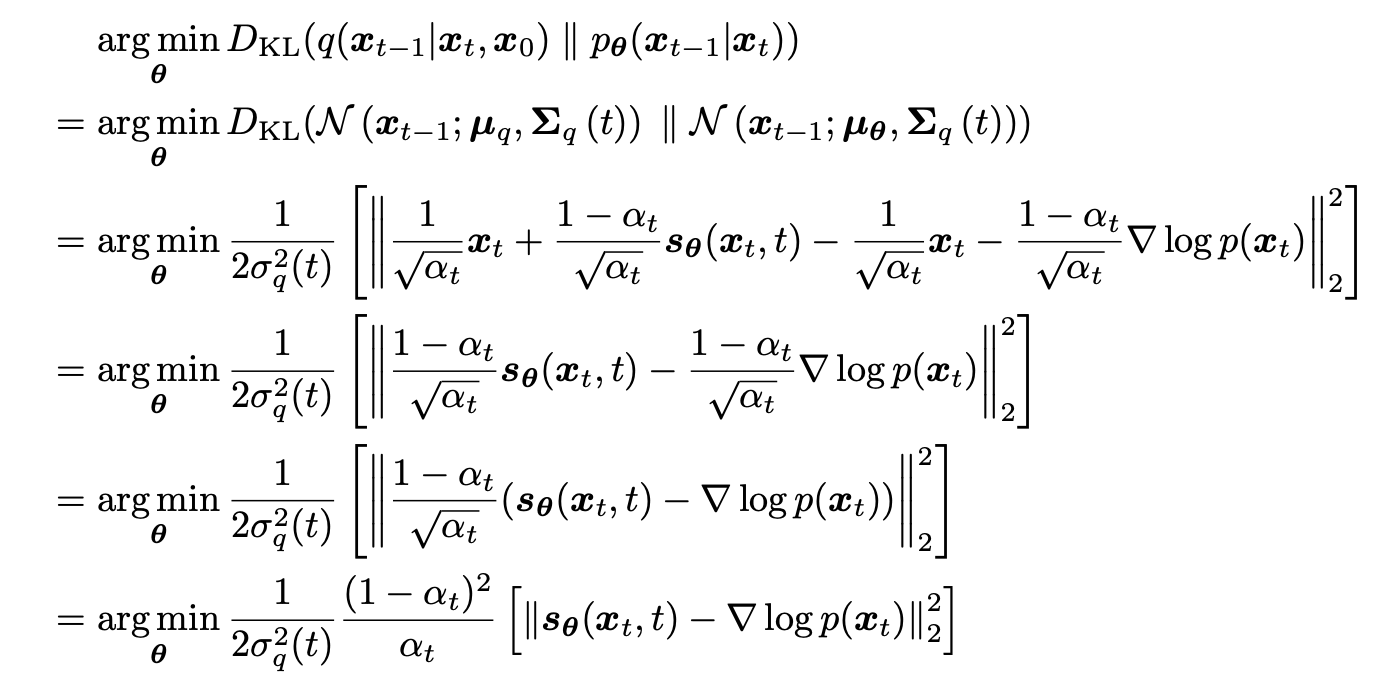
基于分数的生成模型 Score-based Generative Models
首先从 Yann LeCun 等人提出的 energy-based models 开始分析,任意概率分布可由如下形式表示:
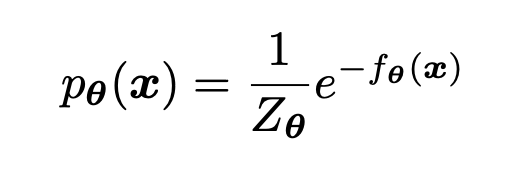
其中, 是 energy function, 是标准化常量。
标准化常量的作用是确保:
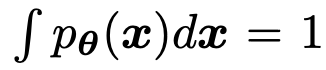
从而得出:
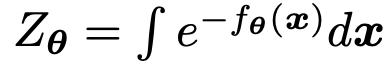
直接对 进行最大似然估计是不现实的,因为对于复杂的 energy function,很难找出对应的标准化常量来进行优化,因此一种可能的解决方式是,使用神经网络 来学习 score function。
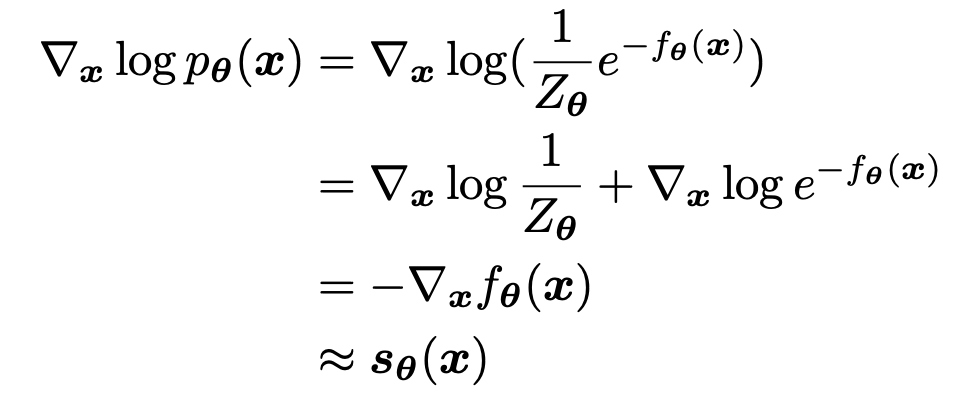
分数模型可以通过最小化二者之间的 Fisher Divergence 来优化:
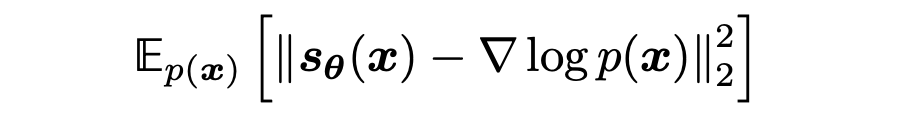
其中,score function 的真实标签 描述在数据空间中使似然增加的方向。
引入朗格文动力学公式:
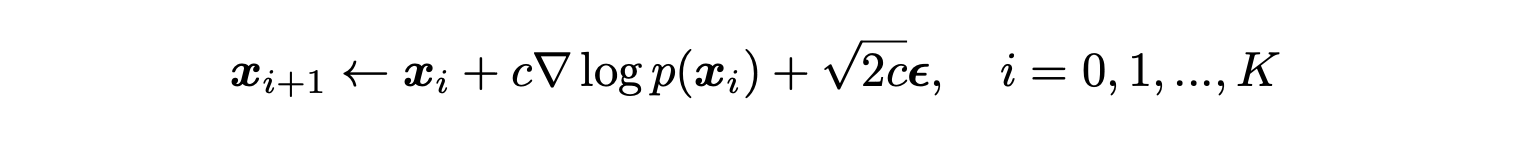
使用 score function 来表示分布并通过马尔可夫蒙特卡罗技巧进行采样成为 Score-based Generative Modeling。
引导 Guidance
到目前为止,文章的重心都放在真实数据的分布 上,但我们通常更加关注某些条件下的真实数据分布 。这可以让我们在一定程度上控制生成的图片。
一个很自然的想法就是在每一噪声等级的时间步上都加上条件信息,于是有
可以是文本,可以是其他图片,也可以是一个类别。对应到上述阐明的 VDM 的三种解释,VDM的目标就变成了:
目前有两种主流的 Guidance 方式,分别是 Classifier Guidance 和 Classifier-Free Guidance。
Classifier Guidance
以 score-based model 为例,通过贝叶斯法则,可以得到:

该式可以理解为无条件分数和一个分类器 的梯度。
为了更加细粒度地控制条件的重要程度,还会加上一个超参数 ,于是就有
当 时,就是无条件的扩散生成;当 很大时,模型的生成会更加依赖于条件信息,同时会损失生成结果的多样性。
Classifier Guidance 的缺点是需要处理任意噪声输入,因此没有可以直接使用的预训练好的 classifier,需要和 VDM 一起进行训练。
Classifier-Free Guidance
Classifier-Free Guidance 的方案不需要单独的分类模型。对 Classifier Guidance 的公式进行移项得到:
将其代入 Classfier Guidance 的公式中,消去 noisy classifier 项可以得到:
同样, 是一个控制学习的条件模型对条件信息的关注程度的超参数。
当 时,学习的条件模型完全忽略条件器并学习无条件扩散模型;当 时,该模型在没有指导的情况下显式地学习条件分布;当 时,扩散模型不仅优先考虑条件得分函数,而且在远离无条件得分函数的方向上移动。换句话说,它降低了生成不使用条件信息的样本的概率,有利于显式地使用条件信息的样本。
由于学习两个独立的扩散模型开销过大,利用 Classifer-Free Guidance 可以同时训练条件依赖和无条件扩散模型。无条件扩散模型可以通过用诸如零的固定常数值替换条件信息来训练,本质上是对条件信息进行 dropout。