[NeurIPS 2017] Attention Is All You Need
Transformer是Sequence-to-Sequence (Seq2Seq) 模型,模型的输入是向量序列,输出同样是向量序列,且输出的长度由模型经过学习决定。
整体结构
Transformer由Encoder和Decoder组成,编码器和解码器都包含6个Block,整体结构如下图所示。
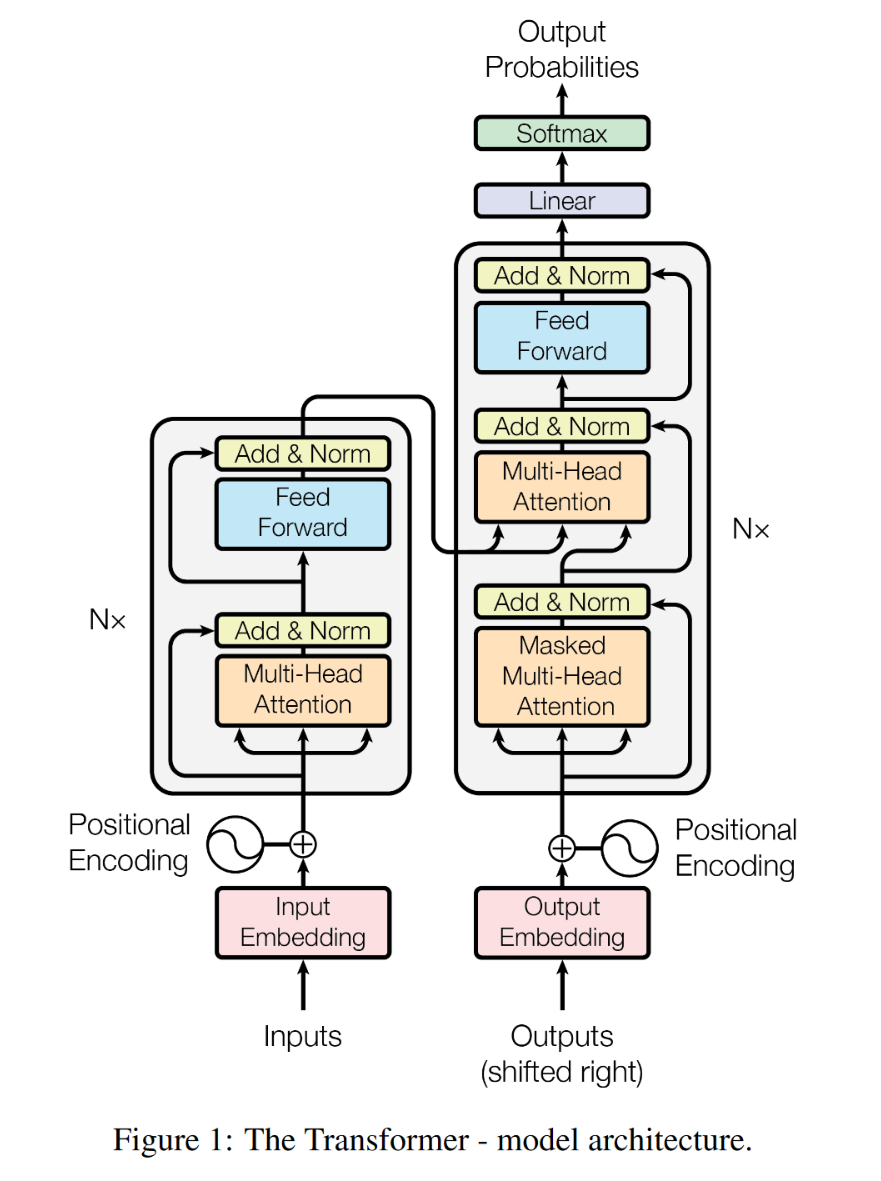
Encoder
整体结构
Transformer Encoder结构如下图所示。其中,Add指的是残差连接Residual Connection,Norm指的是Layer Normalization。
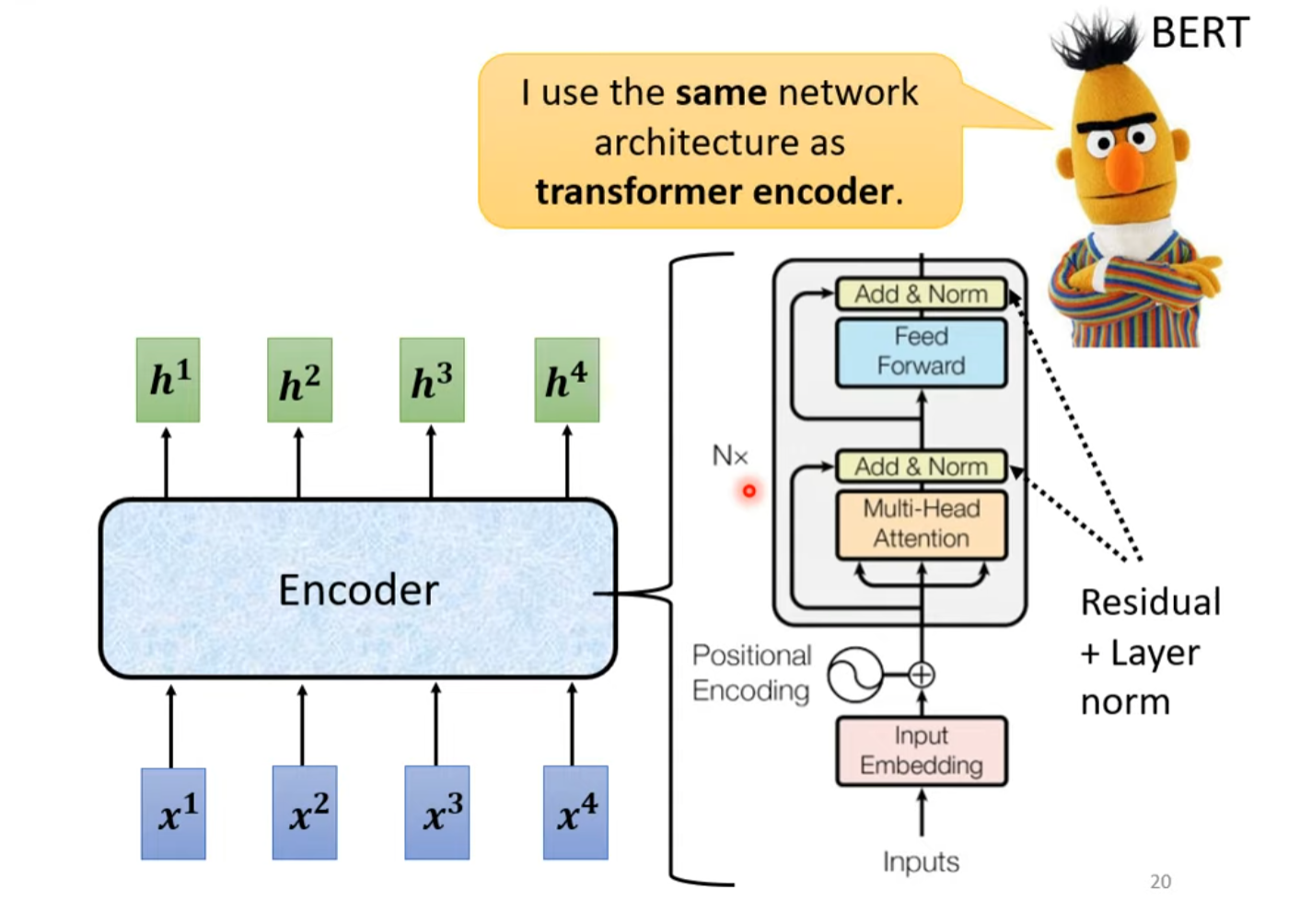
位置编码(Positional Encoding)
对于输入的句子,对一个词汇的嵌入向量的��奇数维度使用sine函数进行编码,对偶数维度使用cosine函数计算编码。
公式如下所示,其中指的是该词汇在整个输入句子中的位置,以及指的是该词汇的嵌入向量中的维度,指的是在嵌入层之后嵌入向量的总维度。即对于每个输入词汇,都要计算次位置编码。
根据三角函数的性质,对于位置的嵌入向量的某一维度(或)而言,可以表示为位置与位置的嵌入向量的与维度的线性组合,使得位置向量中蕴含了相对位置的信息。
最终,位置编码向量的维度与词汇的嵌入维度相同,进行element-wise的相加操作。
具体结构
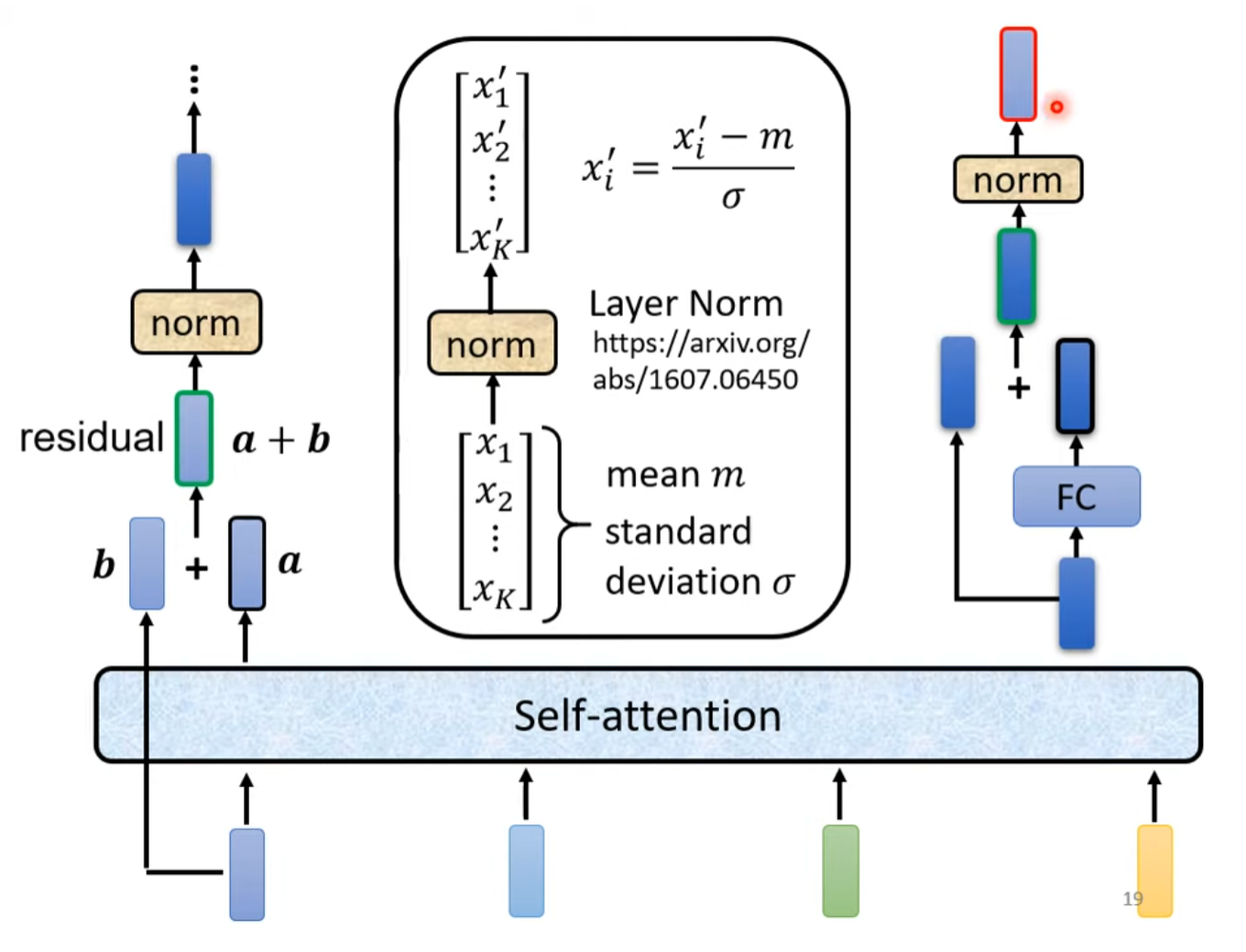
输入向量由Word Embedding和Positional Embedding相加得到。输入序列经过Mutil-Head Self-Attention之后,通过Residual Connection加上自身的输入向量,再经过Layer Normalization,之后送入FCN并进行Residual Connection加上送入FCN的输入自身,最终再进行Layer Normalization,以上构成了一个Encoder Block。每一个Block输出的向量序列长度等于输入的向量序列长度。
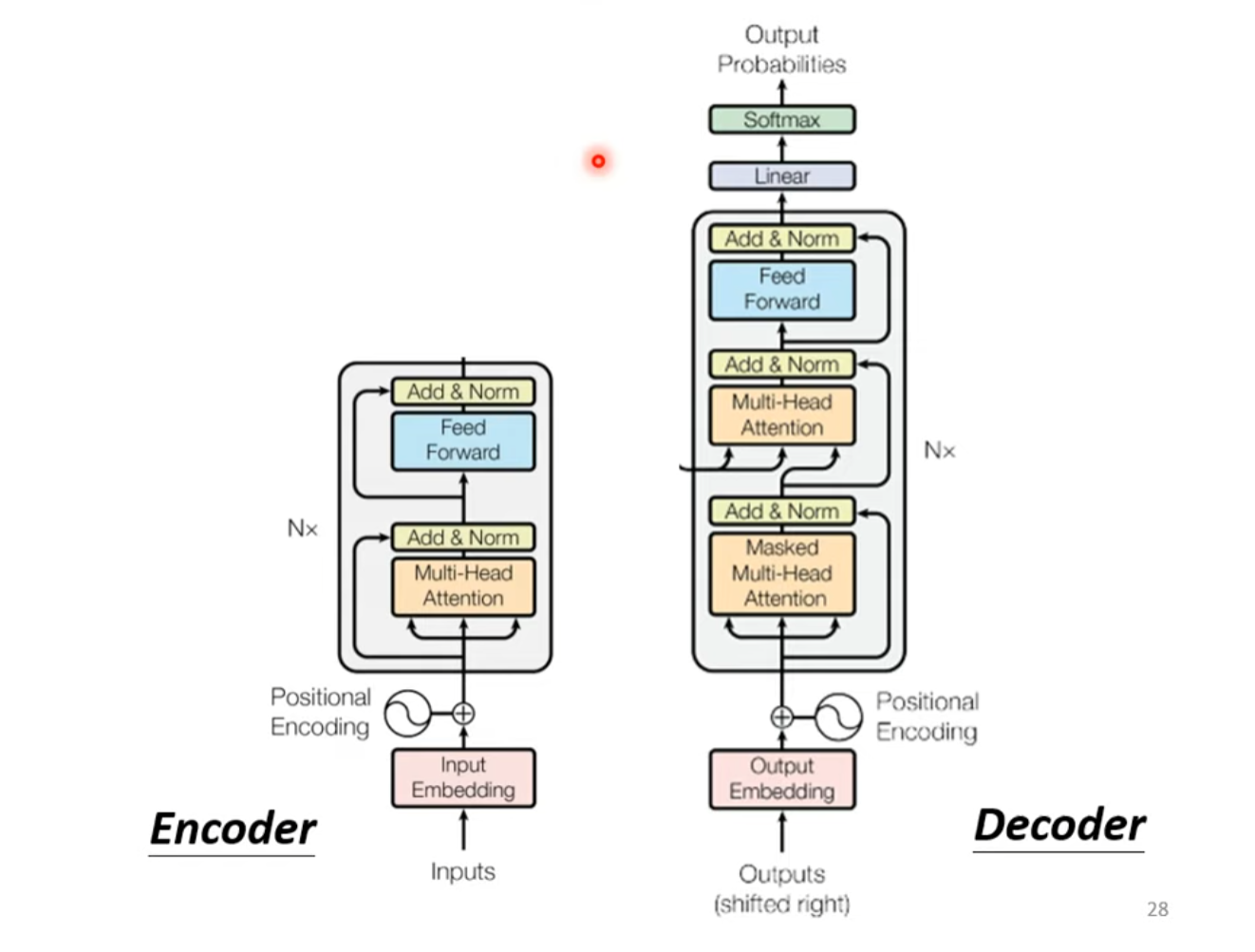
Decoder
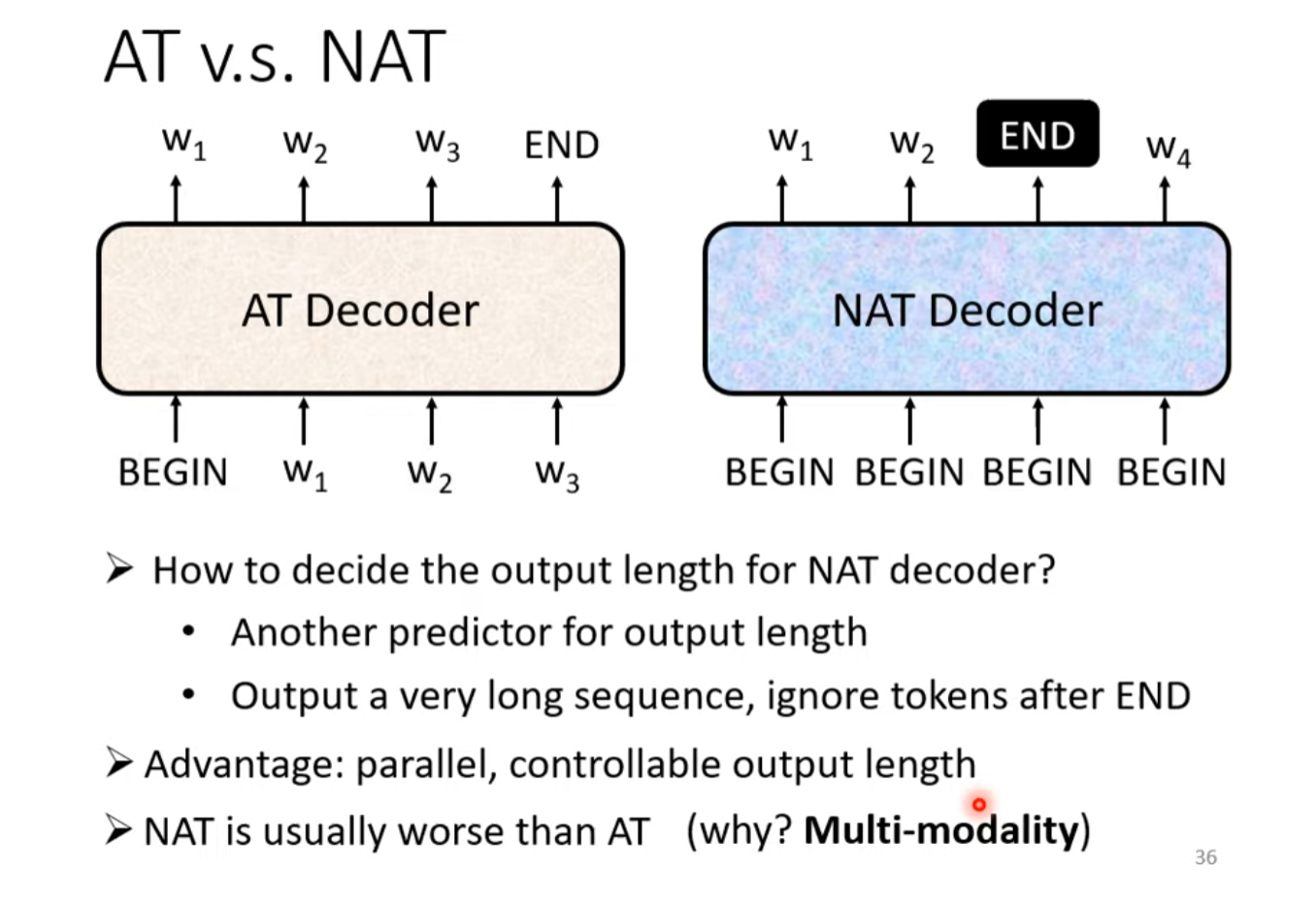
Decoder的任务是生成输出,可以根据是否一次性生成输出分为Autoregressive(自回归,abbr. AT)以及Non-Autoregressive(非自回归,abbr. NAT)两种模式。
自回归类型的Decoder需要逐步生成输出,并将之前自身输出的所有词汇经过嵌入层后生成token作为下一次的输入,通常每次生成一个词或一个符号。这种方式的缺点是需要保存和更新词表中的所有可能选项,因此在大词汇表上可能会变得非常慢。然而,它的优点是能够利用上下文信息来生成输出,这有助于提高翻译的质量。
非自回归类型的Decoder试图在一次操作中生成整个输出序列。这通常通过使用诸如注意力机制等策略来实现,这些策略允许解码器关注输入序列的不同部分,同时生成输出序列的不同部分。NAT的优点在于其高效性,因为它不需要保存和更新大量的可能选项。然而,由于它不能利用上下文信息来生成输出,因此其生成的输出质量普遍会低于AT。
Autoregressive Decoder(AT)
整体结构
词汇表(Vocabulary)
词汇表(Vocabulary)是一个包含了在特定语言或任务中所有可能出现的所有单词或标记的集合。在自然语言处理(NLP)中,词汇表是训练模型时所使用的唯一单词的集合,由具体的生成任务而确定。
Decoder每一步的输出是一个经过Softmax的Probability Distribution(概率分布),代表着词汇表中每一个词汇当前生成的概率,取最大概率值的词汇便是模型当前时间步输出的词汇。
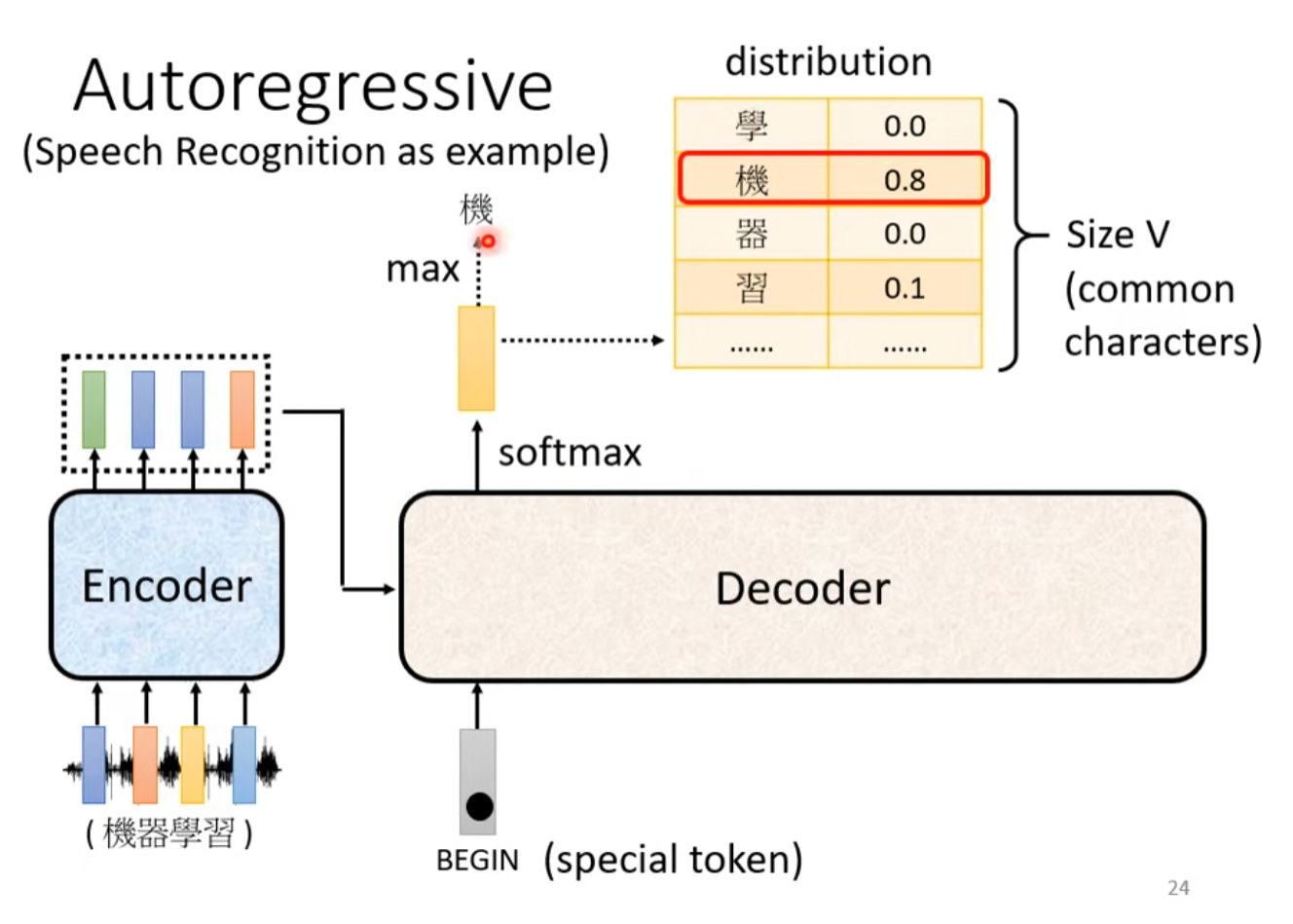
Begin符号
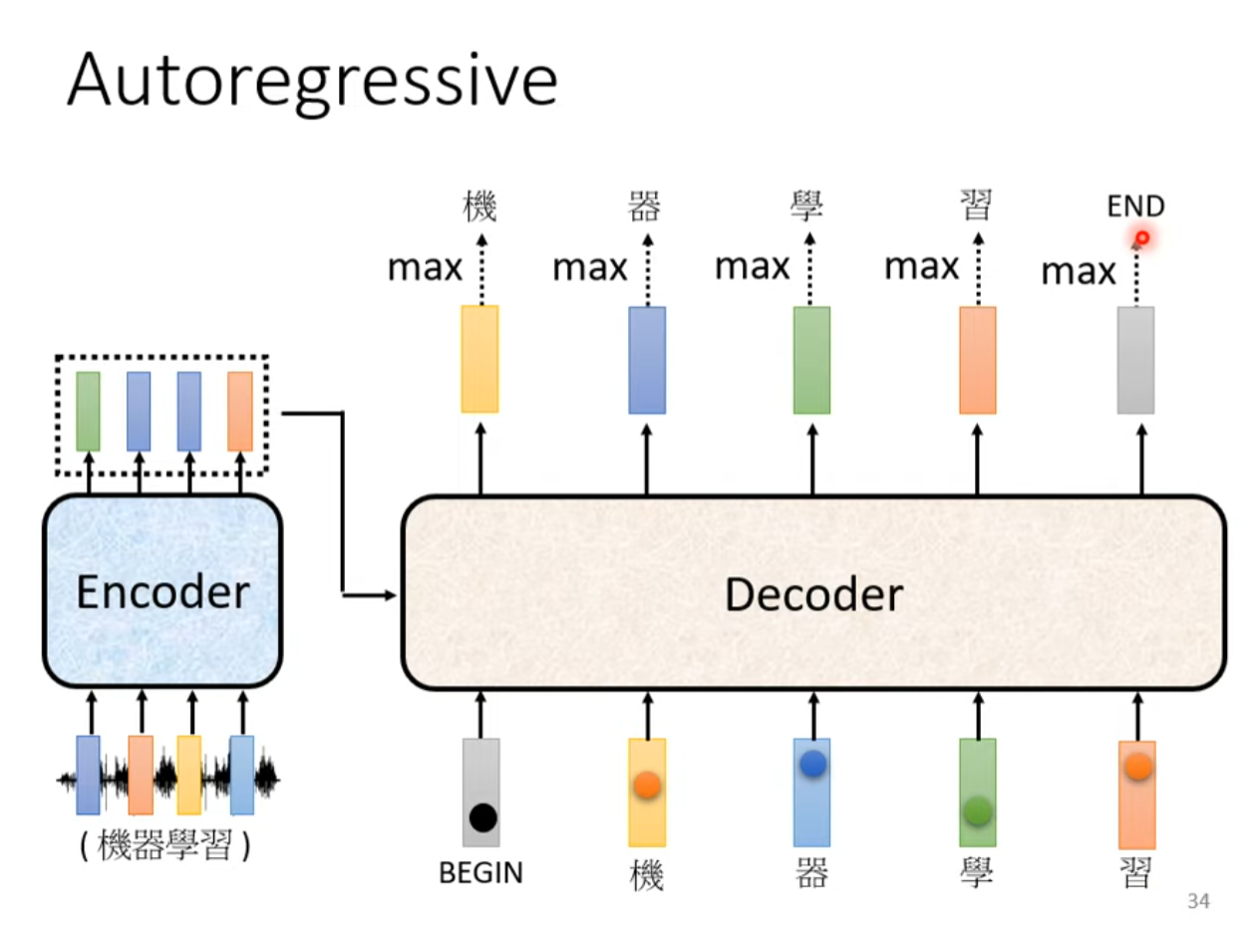
解码器(Decoder)在每个时间步(或每个解码步骤)的输入都来自于前一个时间步自身的输出以及编码器(Encoder)的输出。特别地,首个时间步的输入是Begin符号以及编码器(Encoder)的输出,在每个后续的时间步,解码器的输入会是前一个时间步自身的输出以及编码器(Encoder)的输出,直到生成序列的结束。
Begin符号是在Lexicon中添加的特殊符号,用来表示Decoder生成的开始。Begin符号通常被嵌入到一个低维的连续向量空间中,这个向量空间是通过嵌入层(Embedding Layer)学习得到的,在嵌入层中,离散的符号被映射到一个实数向量。
Begin符号又叫Start符号或SOS符号(Start Of Sentence),都是表示生成的开始。End符号又叫EOS符号(End Of Sentence)。
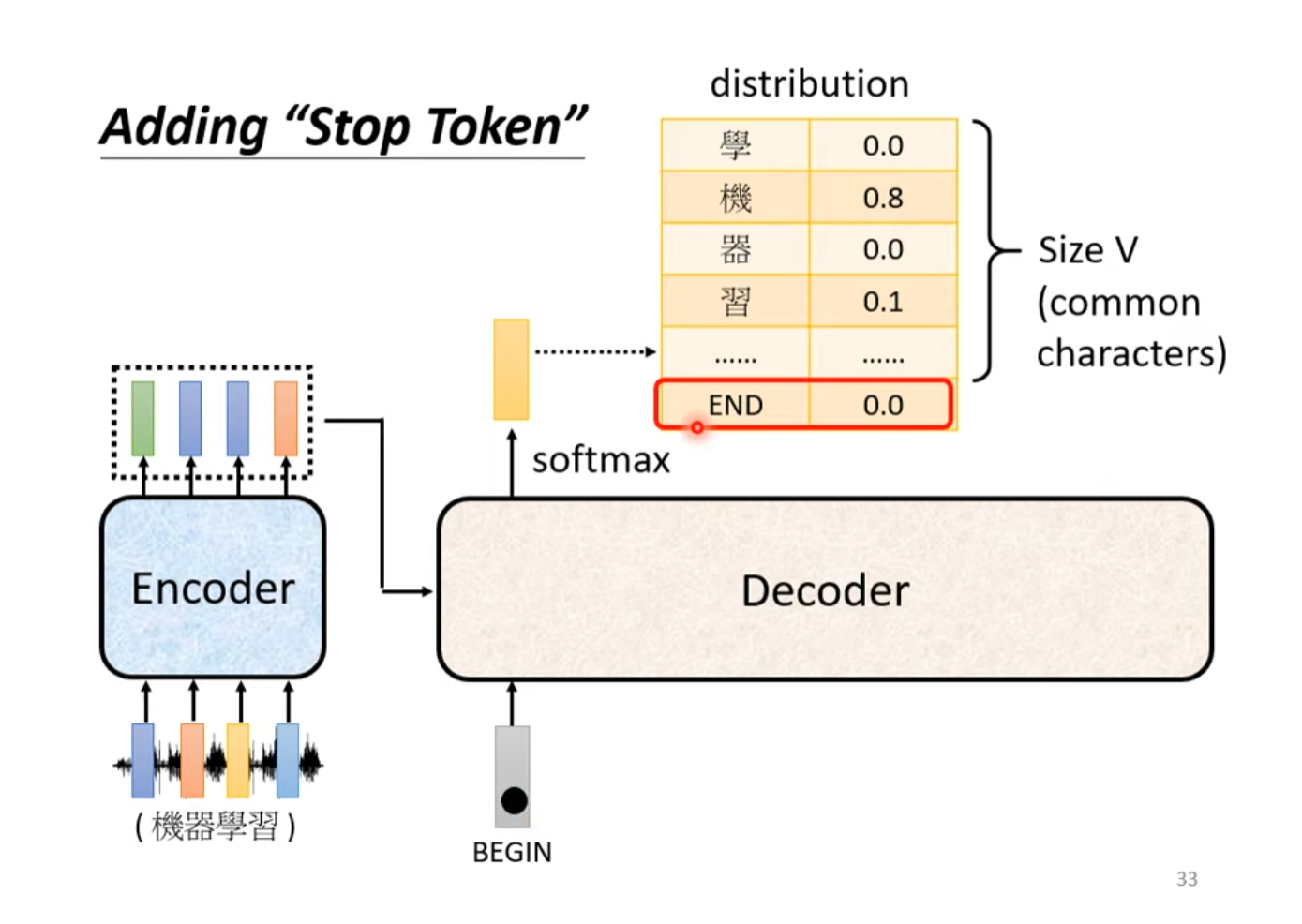
End符号
在Decoder的生成中,每一个时间步的输出是词汇表中每一个单词经过Softmax之后的概率分布。为了保证生成任务可以通过模型自己停止而不是一直重复,我们向Decoder的输出中加入End符号的生成,即每一次输出除了词汇表的所有词汇外还有End符号的概率,当End符号是在所有词汇中概率最大的词汇时,生成停止。
掩码多头自注意力机制(Masked Multi-Head Self-Attention)
掩码多头自注意力与Transformer训练时采取的Teacher Forcing策略有很大的关系,具体分析见下文《Teacher Forcing与Masked Multi-Head Self-Attention》的讨论环节:Teacher Forcing与Masked Multi-Head Self-Attention
观察Decoder的整体结构,掩码多头自注意力的输入是添加位置编码之后的Decoder当前时间步之前的所有输出单词经过嵌入后的向量表示。
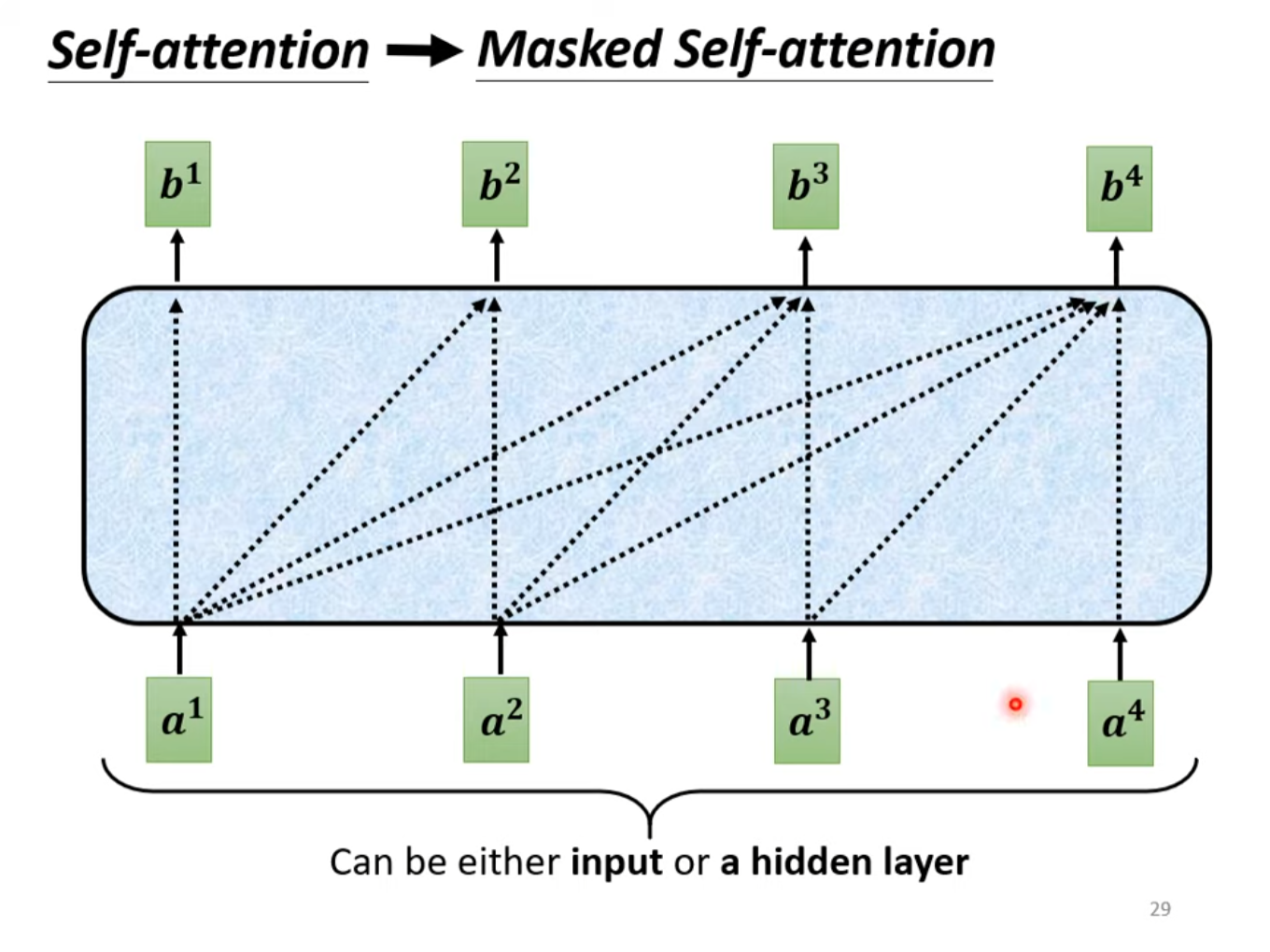
掩码多头自注意力机制用于确保在生成序列的过程中,每个位置只能关注到该位置及其之前的位置。这是通过在Self-Attention的计算中应用一个掩码(mask)来实现的。这确保了在生成序列时,每个位置只能查看到它之前的信息,而不能查看到未来的信息,从而实现了自回归性质。
具体来说,添加掩码后的自注意力机制在生成注意力分数时不再考虑输入序列的所有向量。如在输入向量在计算注意力分数时,只将的query向量与至的个key向量做dot product,而不考虑之后的输入的key。
对于第个时间步,Masked Mutil-Head Self-Attention的输入是时间步之前Decoder生成的所有输出单词的嵌入表示。
交叉注意力(Cross-Attention)
交叉注意力是连接Encoder和Decoder的桥梁,也是Decoder输入的重要组成部分。
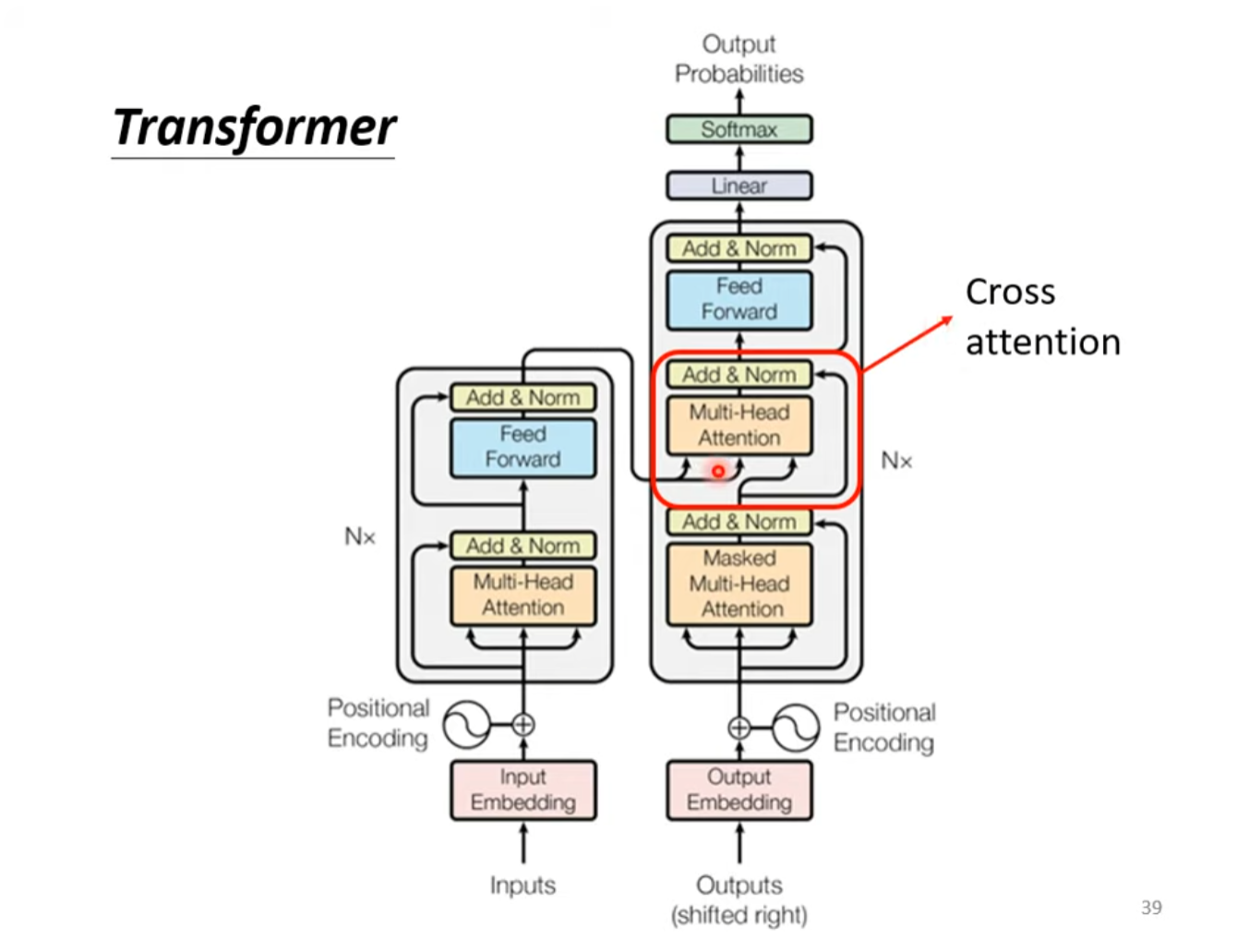
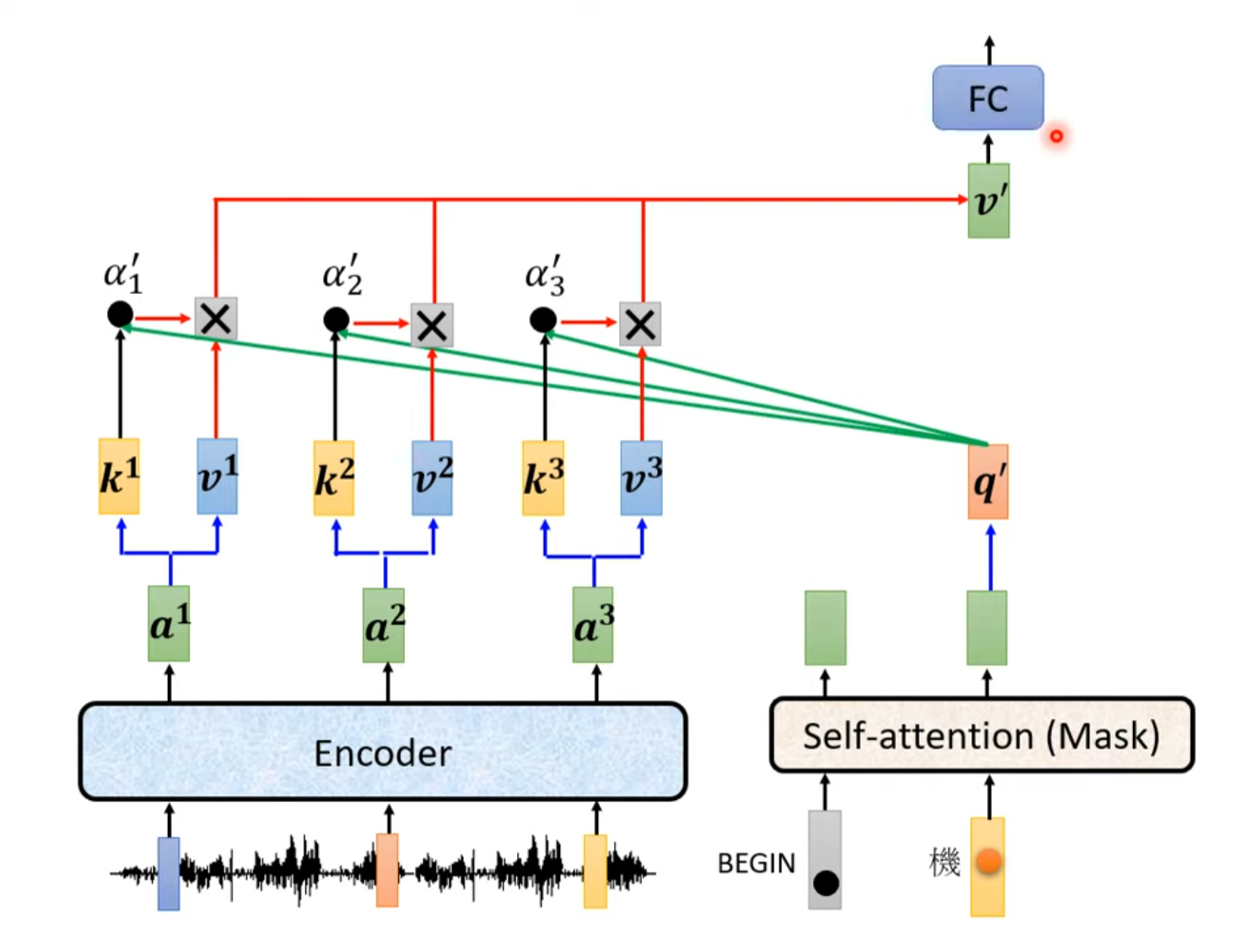
交叉注意力接收两个输入序列,一个来自编码器(Encoder)的输出序列(通常是输入序列的表示),另一个来自解码器(Decoder),是经过掩码多头自注意力机制的输出序列(通常是正在生成的序列的中间表示)。
在交叉注意力中,每次计算注意力得分的query来自解码器,key和value来自编码器。解码器每个向量的查询(Query)与编码器位置的键(Key)进行点积得到了注意力分数,通过Softmax操作后转换为注意力权重,再与编码器位置的值(Value)weighted sum得到加权注意力分数,最终将加权注意力分数求和得到每个输入向量的输出。
Non-Autoregressive Decoder(NAT)
训练(Training)
损失函数
在 Transformer 中,Encoder 不像 Decoder 需要生成序列,因此它通常不涉及标签的预测。Encoder 的训练通常是在整个模型中的联合训练中进行的,通过优化整个模型的损失函数来进行。
Transformer 的整体训练过程一般分为以下几个步骤:
- 编码器(Encoder)的正向传播: 输入序列经过编码器的正向传播,产生一组上下文表示。
- 解码器(Decoder)的正向传播: 解码器接收上下文表示,并生成目标序列。
- 计算损失: 通过比较生成的目标序列与实际目标序列,计算损失。在 Decoder 中,通常使用交叉熵损失函数。
- 反向传播: 根据损失,进行反向传播,更新模型参数。这个过程中,梯度通过整个模型传播,包括 Encoder 和 Decoder。
整个模型的参数(包括 Encoder 和 Decoder)都是通过最小化整体损失来进行联合训练的。这是因为整体模型需要协同工作,Encoder 的表示对于 Decoder 的性能至关重要。在训练过程中,梯度从损失函数传播回整个模型,包括 Encoder 和 Decoder,从而更新它们的参数。
需要注意的是,Transformer 模型通常使用的是端到端的训练方式,整个模型的参数是一次性更新的。在某些场景下,你可能会看到对 Encoder 或 Decoder 进行微调(fine-tuning)的情况,但这是在特定应用场景下的调整,不是 Transformer 模型的标准训练方式。
Teacher Forcing
在Transformer的推理阶段,自回归类型的Decoder根据分词方式的不同,一个词汇一个词汇的输出,将当前时间步之前生成的所有词汇作为输入load进入Decoder中。但在训练时如果遵从同样的生成范式会大大降低效率,并且面临则一步错步步错的风险(Error Propagation)。
因此使用Teacher Forcing策略,将Ground Truth一次性喂到Decoder中,使模型更快收敛并且避免误差积累的问题。
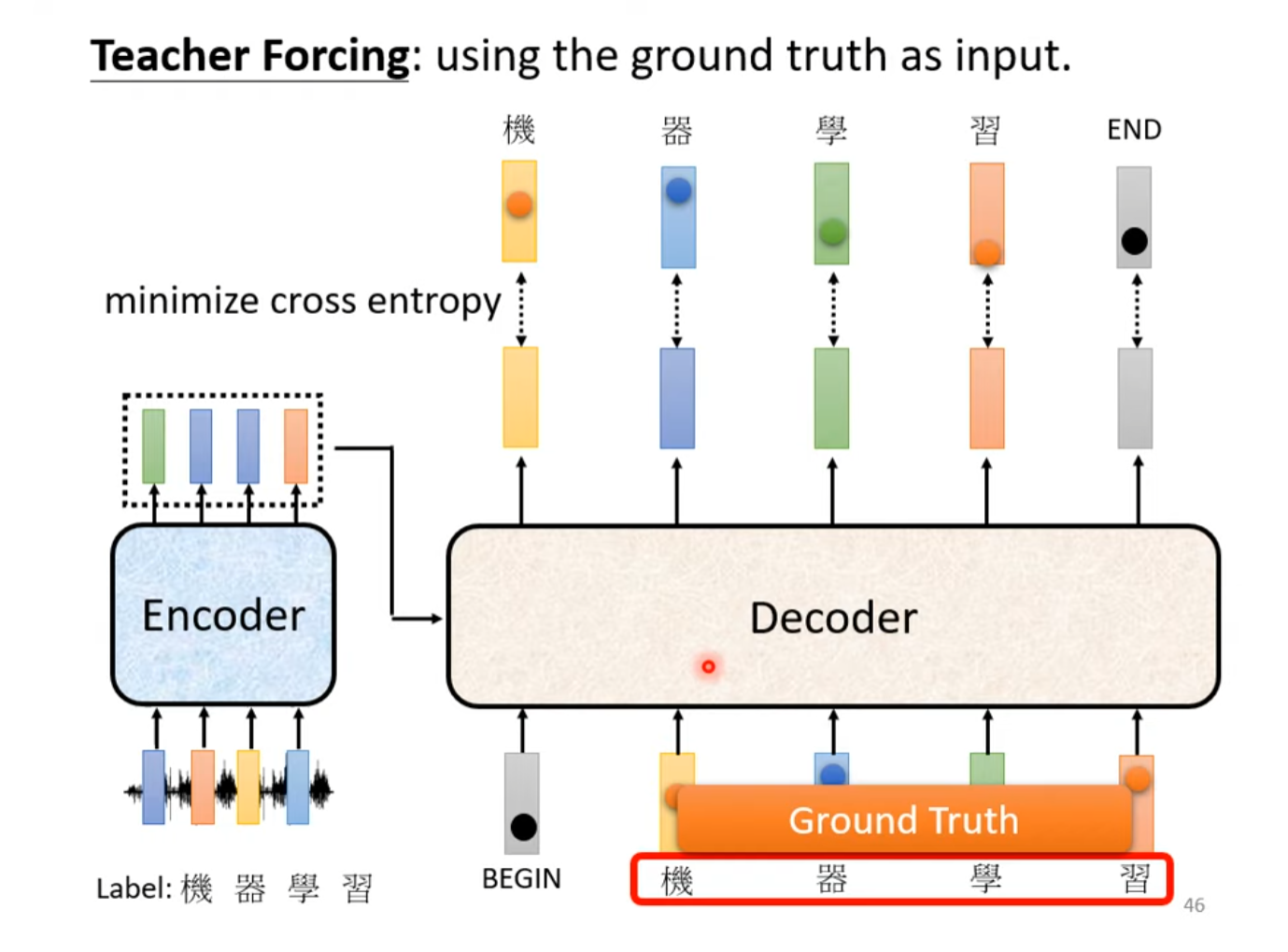
但是,自回归Decoder在推理时是一个一个词汇产生的,在产生第个词汇时其后续的词汇是未知的,更不用说进行注意力分数的就算了,而在训练过程中使用Teacher Forcing时却可以得到第个及其之后词汇的注意力信息,如果不添加其他策略显然会对模型的泛化能力造成很大的影响,而且这并不符合自回归(Autoregression)的特性。为了解决这个问题,掩码多头注意力机制应运而生,在训练阶段将模型在时间发展顺序的右侧的输入masked掉,防止模型学习到不该学习的注意力。
Teacher Forcing与Masked Multi-Head Self-Attention
参考文献:MultiHead-Attention和Masked-Attention的机制和原理
与Encoder的多头自注意力不同,在Decoder中,为注意力机制应用了掩码,使模型只能关注到当前位置及其之前的位置,而不能访问��未来的信息。这解决了引入Teacher Forcing出现的问题,避免了训练与推理阶段的Mismatch,维护了自回归的特性。
具体来说,模拟推理过程中第一个词汇时的场景。当模型只有词汇向量输入时,在Decoder中,与自身计算注意力分数,于是有
我们再模拟训练过程中使用Teacher Forcing,一次性输入为两个词汇与的情况,于是有
然而,为了使训练过程中符合推�理时自回归的特性,理想的输出应该是
继续扩展,当有个输入词汇时,应该有
因此,我们需要将当前时间步计算的词汇的时间顺序右侧的输入词汇全部掩码,置为0。
在源码中,有如下片段实现掩码:
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
在源码中,将mask置为负无穷是因为这是在经过Softmax之前进行的掩码,在经过Softmax之后负无穷小就变成了0。