跳到主要内容

扩散模型（Diffusion Model）

提示

在以前的文章图像生成模型中已经大概介绍了目前SOTA的图像生成模型的共同点，并初步了解了Diffusion Model，在这篇文章中将详细讲解扩散模型的数学原理等。

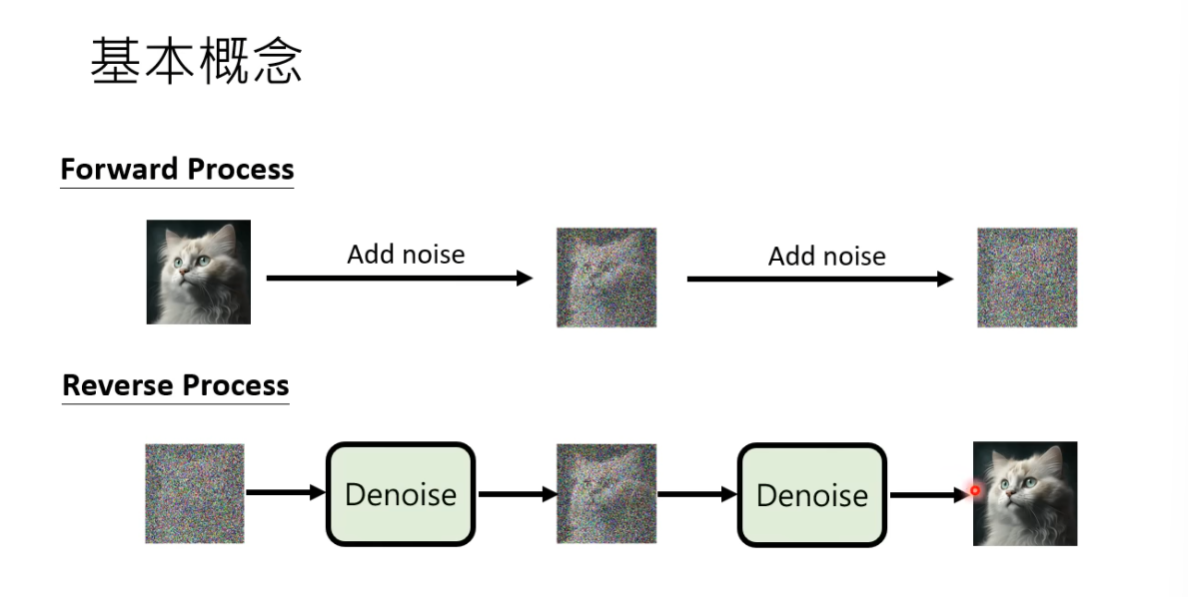
基本概念​

首先回顾一下扩散模型的基本概念和生成过程，可以大概分为两步：

  1. Forward Process：对训练集中的图片不断加入与图片shape相同的、从某随机分布中sample出的噪声，直至图片可以被认为是从该随机分布中sample出的矩阵。

    Forward Process又叫做Diffusion Process，在这一步中产生的噪声-加入噪声的图像对可以用来训练Noise Predictor，即从有噪声的图像中预测出其中的噪声，再从输入中减去噪声得到降噪后的图片。

    图像生成的原理

    这一步的目的也同样在之前的文章图像生成模型中提到过：由于根据文字prompt期待生成的图像并不是固定的，可以认为生成的图片在目标域（Target Domain）符合某种分布。因此目前的SOTA模型除了将文字prompt作为输入，还从某随机分布中sample出图片shape的随机向量（矩阵）作为输入，期待模型根据prompt将源域（Source Domain）输入的随机向量映射到目标域的分布，生成对应的图片。

  2. Reverse Process：使用Diffusion Process训练的Noise Predictor，根据文字Prompt对从随机分布中sample出的图片大小的噪声图片进行降噪，得到原图。

image-20231202192659531

值得注意的是，变分自编码器（Variational Auto-Encoder, abbr. VAE）与Diffusion Model非常相似：VAE对训练集中的原始图像使用Encoder将其变换为某种Latent Representation，这种Latent Representation的分布也是符合某种随机分布的，VAE再通过Decoder将期待生成的目标域图像还原出来。

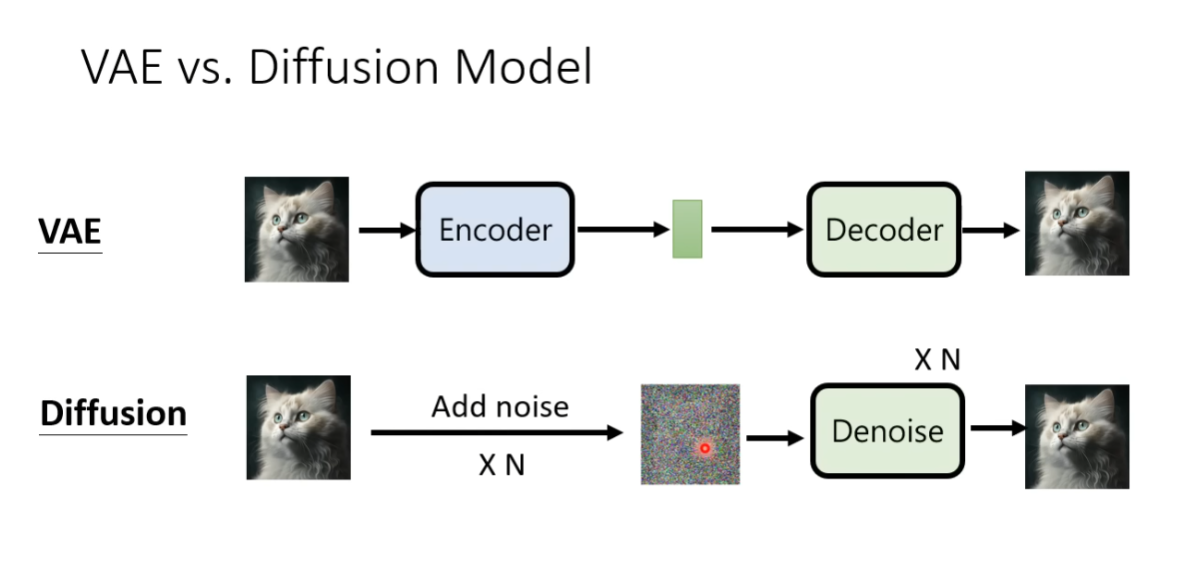
image-20231202222644684

在下面的文章中我们也会学习一下VAE的数学原理，从VAE到Diffusion Model的具体数学推导，可以参考胡老师推荐的论文Understanding Diffusion Models: A Unified Perspective。

下面我们以DDPM论文中的原图来分析DDPM的训练与推理过程。

image-20231202232526449

训练过程​

  1. 循环开始，重复以下步骤；

  2. 首先从数据集中sample出原始图像x0\mathbf{x}_0；

  3. tt是从1,…,T1,\ldots,T范围中sample出的一个integer；

  4. ϵ\epsilon是从Normal Distribution中sample出的与x0\mathbf{x}_0相同大小的噪声；

  5. 根据如下规则进行梯度下降，训练Noise Predictor：

    ∇θ∥ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)∥2(1)\nabla_{\theta}\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\theta}(\sqrt{\bar{\alpha}_{t}}\mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}}\boldsymbol{\epsilon},t)\right\|^{2}\tag{1}

    首先对x0\mathbf{x}_0和ϵ\epsilon根据权重αˉ1,αˉ2,...αˉT\bar{\alpha}_1,\bar{\alpha}_2,...\bar{\alpha}_T做weighted sum产生加入噪声后的图像。通常来说，αˉ1\bar{\alpha}_1至αˉT\bar{\alpha}_T是递减的，当在第2步中sample到的tt越大，则原始图像x0\mathbf{x}_0对新图像的贡献越大。

    ϵθ\epsilon_{\theta}是Noise Predictor，其输入是加入噪声的图像以及sample出的tt，而ϵθ\epsilon_\theta训练的Ground Truth就是第3步中sample出的噪声ϵ\epsilon；

  6. 直至噪声预测模型ϵθ\epsilon_\theta训练至收敛。

image-20231202235322516

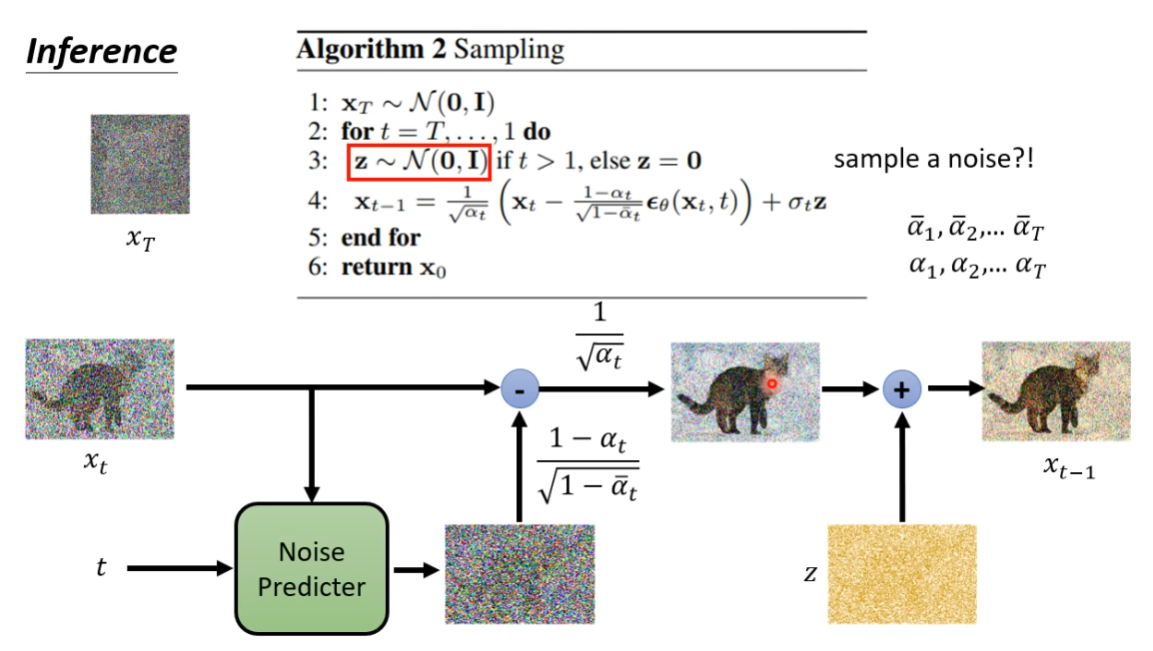
推理过程​

  1. 从Normal Distribution中sample出图片大小的噪声xT\mathbf{x}_T；

  2. tt从T,…,1T,\ldots,1范围循环TT次；

  3. 对与每一次以tt计数的循环，若t>1t>1，则从Normal Distribution中sample出z\mathbf{z}，否则z=0\mathbf{z}=\mathbf{0}；

  4. 根据如下公式得到降噪后的图像：

    xt−1=1αt(xt−1−αt1−αˉtϵθ(xt,t))+σtz(2)\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\boldsymbol{\epsilon}_{\theta}(\mathbf{x}_{t},t)\right)+\sigma_{t}\mathbf{z}\tag{2}

    其中，xt\mathbf{x}_t代表上一步骤中输出的降噪后的图像，xt−1\mathbf{x}_{t-1}代表当前步骤即将输出的降噪后的图像，ϵθ\epsilon_\theta代表Noise Predictor预测出的噪声，αˉ1,αˉ2,...αˉT\bar{\alpha}_1,\bar{\alpha}_2,...\bar{\alpha}_T以及α1,α2,...αT\alpha_1,\alpha_2,...\alpha_T是两组权重序列；

  5. 结束本次for循环；

  6. 当t=1t=1时，得到x0\mathbf{x}_0，即最终降噪后的图像。

image-20231203133323788