数字图像处理复习笔记

tip

本笔记使用的教材是陈天华所著、清华大学出版社的《数字图像处理及应用：使用MATLAB分析与实现》。

Take me to church, I'll worship like a dog at the shrine of your lies.

I'll tell you my sins, and you can sharpen your knife.

Offer me that deathless death, good god, let me give you my life.

第2章 数字图像处理基础

图像的采样与量化

为了从模拟图像产生数字图像，需要进行采样与量化，即对模拟图像在空间$(x, y)$方向上以及亮度函数$f(x, y)$进行离散化处理。

• 采样：

  模拟图像在空间$(x, y)$上的离散化称为采样。

  若在x和y方向上均进行等间距的采样，则称为均匀采样。

  采样点的多少以及采样的间隔直接影响着图像的质量。

• 量化：

  模拟图像经过采样后，在时间和空间上被离散化为像素，但采样所得的像素点的像素值依然是连续量。量化过程就是以离散的灰度值信息代替连续的模拟量灰度信息的过程，是一对多的过程。

  量化可以分为线性量化以及非线性量化。

灰度级一般以2的整数次幂表示，如大多图像为彩色RGB图像，256个灰度级，位深度为8（$2^8=256$），则对于分辨率为256×256的图像来说，需要256×256×3×8位表示，即每一个像素实际上使用24位表示。

距离度量

4邻域$N_4(p)$即该像素上下左右的四个点，8邻域$N_8(p)$，对角邻域$N_D(p)$。

像素之间的距离度量必须满足三种关系：

1. 非负性
2. 对称性
3. 三角不等式

三种距离度量：

已知，点$p$的坐标为$(x, y)$，点$q$的坐标为$(s,t)$。

1. 欧氏距离：

   $$D_e(p,q)=\sqrt{(x-s)^2+(y-t)^2}\tag{1}$$

2. 城市距离

   $$D_4(p,q)=\vert x-s\vert+\vert y-t\vert \tag{2}$$

3. 棋盘距离

   $$D_8(p,q)=max(\vert x-s\vert,\vert y-t\vert)\tag{3}$$

图像质量评价

• MSE越小代表待测图像与参考图像越接近，均方误差公式如下：

  $$MSE=\frac{1}{MN}\sum_{x=1}^{M}\sum_{y=1}^{N}[f(x,y)-g(x,y)]^2\tag{4}$$

• SNR：参考图像像素值的平方均值与均方误差的比值的对数的10倍。越大代表图像质量越好

• PSNR：峰值信噪比，图像所允许的最大像素值的平方与均方误差的比值的对数的10倍，这是信噪比的改良版本，消除了图像自身像素值对评价指标的影响。越大代表图像质量越好

• SSIM为结构相似系数，越大代表图像质量越好

灰度直方图

第3章 图像变换

傅里叶变换

可以使用傅里叶变换的函数需要满足狄利克莱条件（Dirichlet Condition）：

1. 具有有限个间断点
2. 具有有限个极值点
3. 绝对可积

傅里叶变换的特性：

important

傅里叶频谱图的特征：

• 频率分布：傅里叶频谱图展示了图像在不同频率下的强度分布。高频部分对应图像中的边缘和细节，低频部分对应图像中的整体结构和大致轮廓。
• 能量分布：图像中不同频率的能量在频谱图中以不同强度的幅度呈现。高幅度的频率分量通常标示着图像中强烈的变化或边缘。
• 平移不变性：傅里叶变换具有平移不变性，这意味着在频域中图像的平移对应于幅度谱中相位的改变而不影响幅度谱本身。

连续傅里叶变换

一维连续傅里叶变换

$$F(u)=\int_{-\infty}^{+\infty}f(x)e^{-j2\pi ux}dx\tag{5}$$

一维连续傅里叶逆变换

$$f(x)=\int_{-\infty}^{\infty}F(u)e^{j2\pi ux}du\tag{6}$$

二维连续傅里叶变换

$$F(u,v)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)e^{-j2\pi (ux+vy)}dxdy\tag{7}$$

二维连续傅里叶逆变换

$$f(x,y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(u,v)e^{j2\pi (ux+vy)}dudv\tag{8}$$

离散傅里叶变换

一维离散傅里叶变换

$$F(u)=\sum_{x=0}^{N-1}f(x)e^{-j\frac{2\pi ux}{N}}\tag{9}$$

一维离散傅里叶逆变换

$$f(x)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)e^{j\frac{2\pi ux}{N}}\tag{10}$$

二维离散傅里叶变换

$$F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (\frac{ux}{M}+\frac{vy}{N})}\tag{11}$$

二维离散傅里叶逆变换

$$f(x,y)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi (\frac{ux}{M}+\frac{vy}{N})}\tag{12}$$

第4章 图像处理的基本运算

点运算

下图展示了点运算的主要应用：对比度拉伸

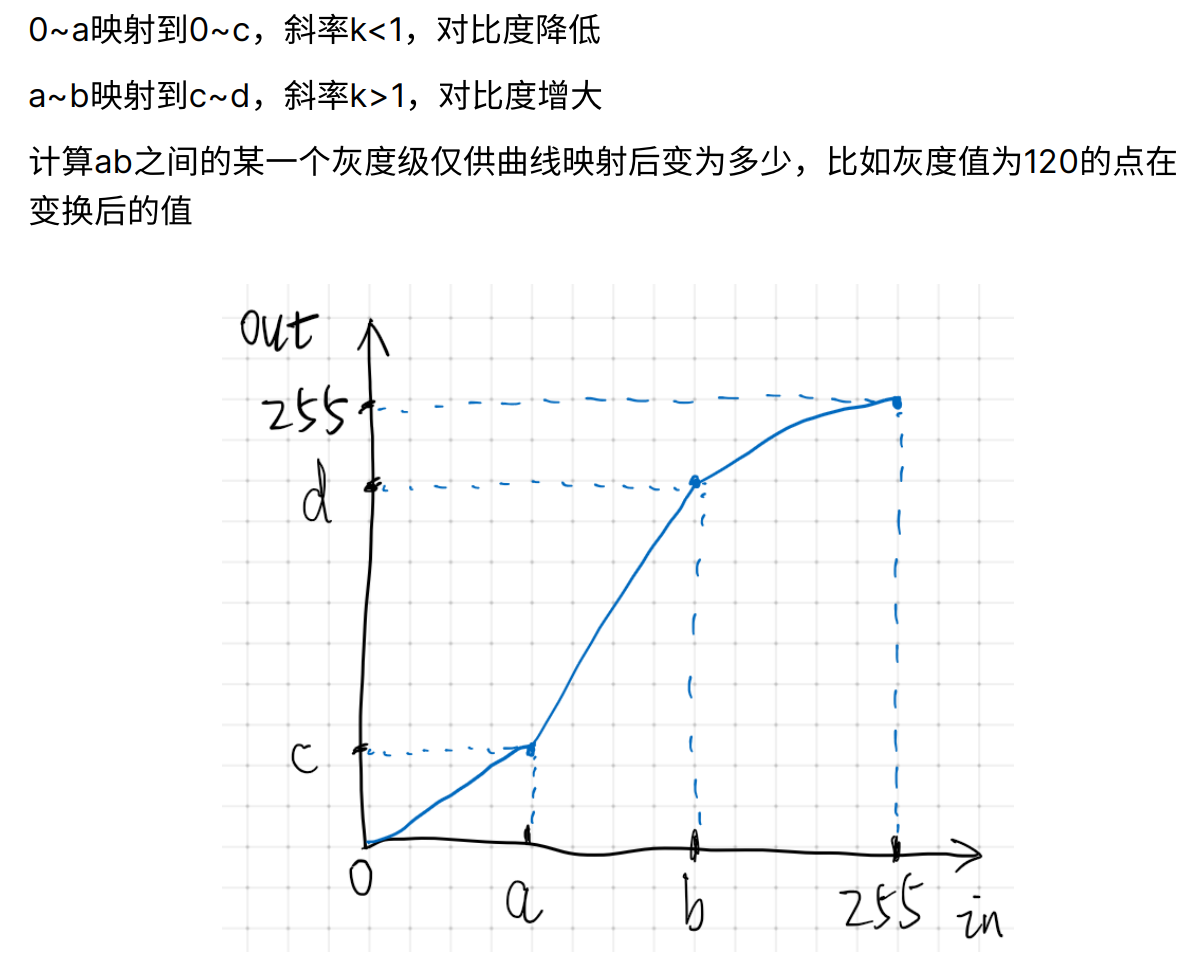
主要应用：

1. 对比度拉伸
2. 光度学标定
3. 显示标定
4. 轮廓线
5. 裁剪

比例缩放

使用齐次坐标对图像进行比例缩放。

全比例缩放是指x方向和y方向使用相同的比例系数。

当对图像进行放大时，会产生之前没有的像素，此时需要使用插值来解决。

灰度级插值

最近邻法插值

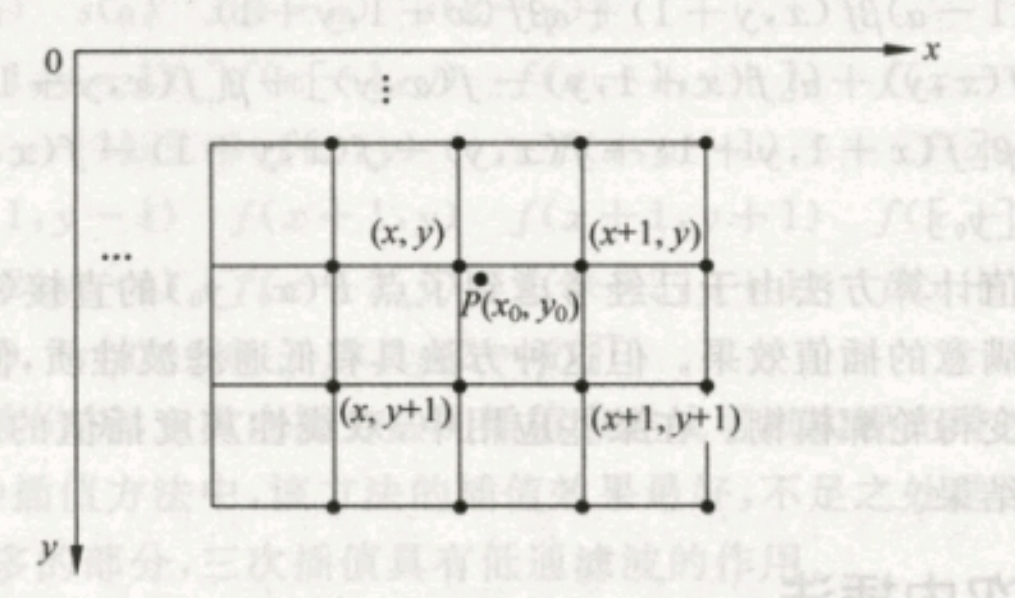
双线性插值（Bilinear）

例题：

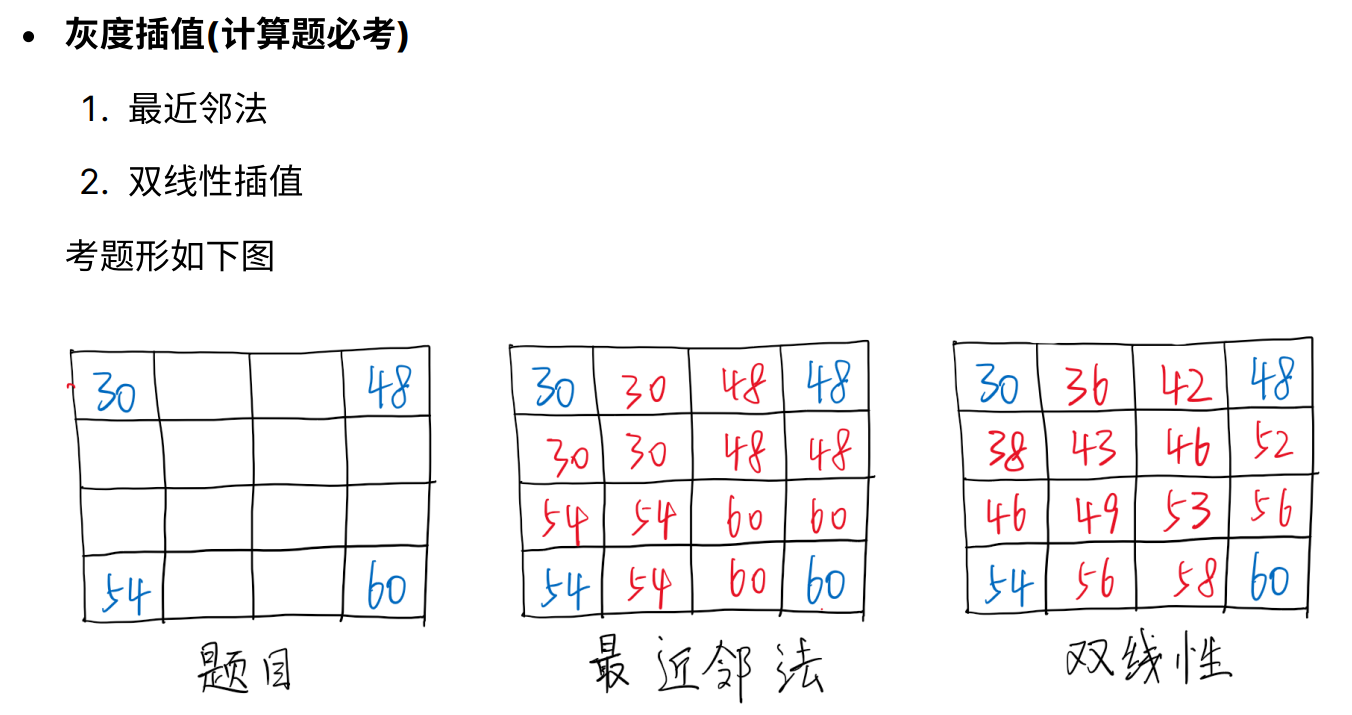
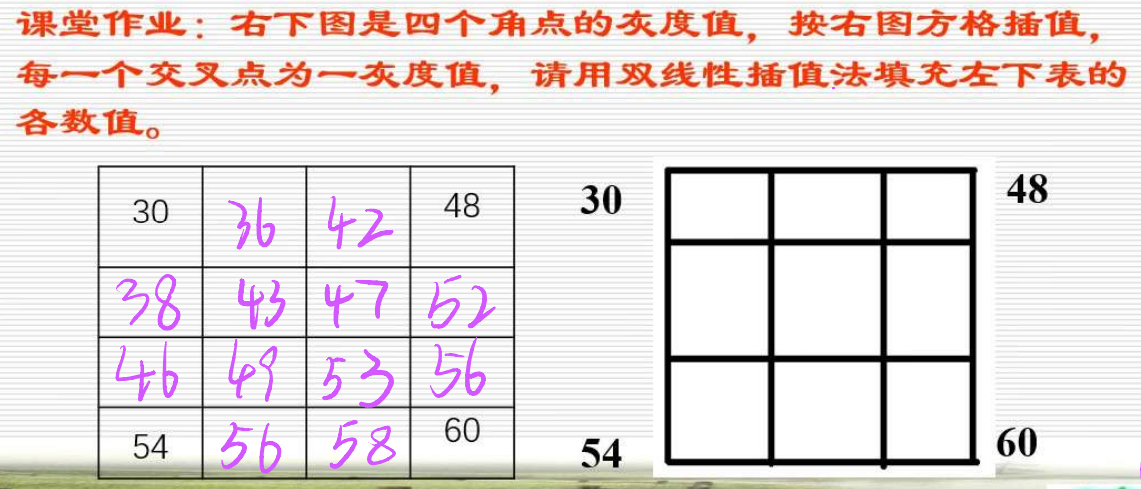
第5章 图像空域增强

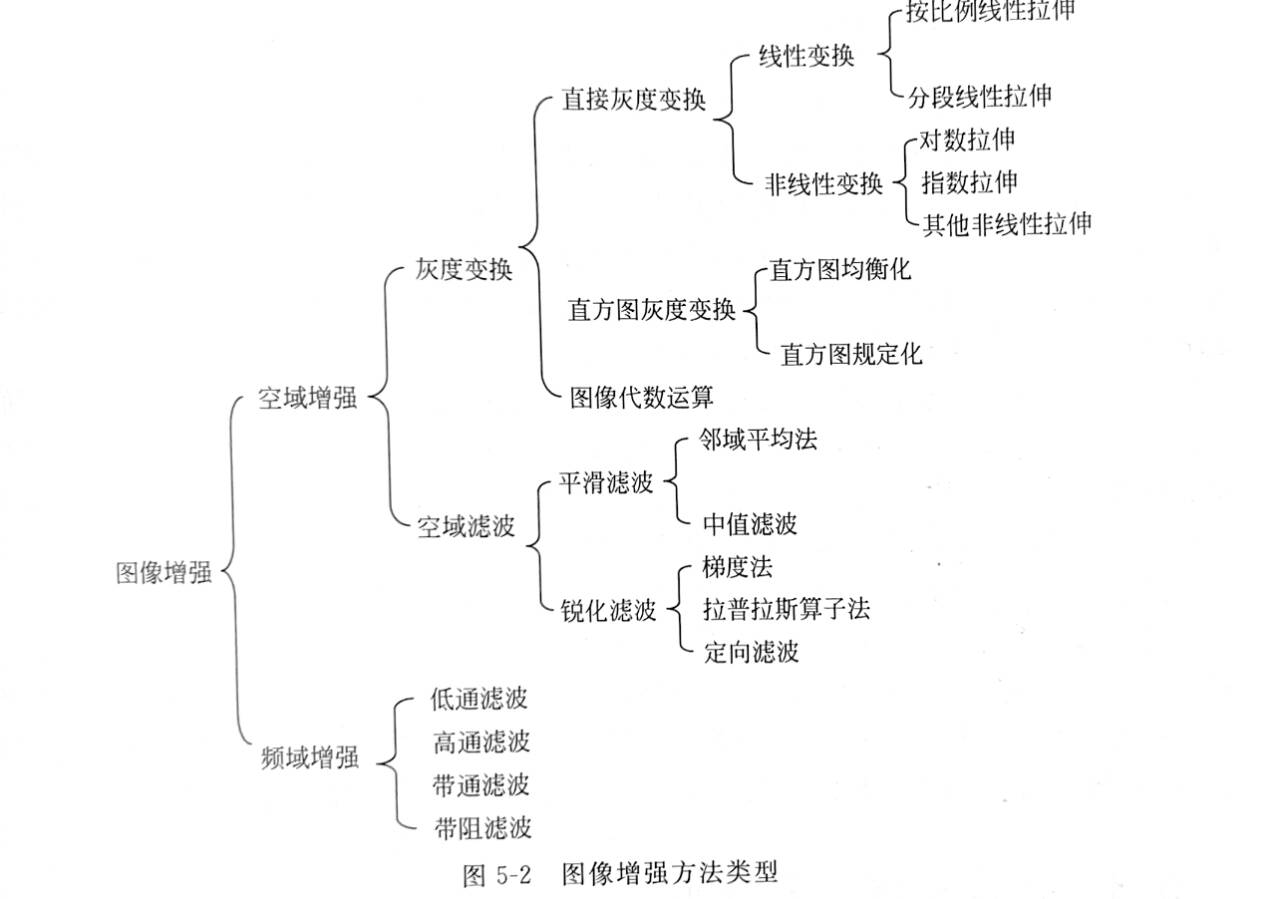
直接灰度变换

线性变换

是指将输入图像的灰度值的动态范围按线性关系变换至指定范围或灰度的整个动态范围。

• 按比例线性变换
  • 均匀线性变换
  • 限幅线性变换
• 分段线性拉伸

非线性变换

• 对数拉伸可以拉伸低亮度区域，压缩高亮度区域。
• 指数拉伸可以拉伸高亮度区域，压缩低亮度区域。

注意，上述的拉伸是指新的图像在该灰度范围内分布的更均匀，即出现的灰度级更多；压缩的意义是指新的图像在该灰度范围内分布的更狭窄，即出现的灰度级更少。

例题：

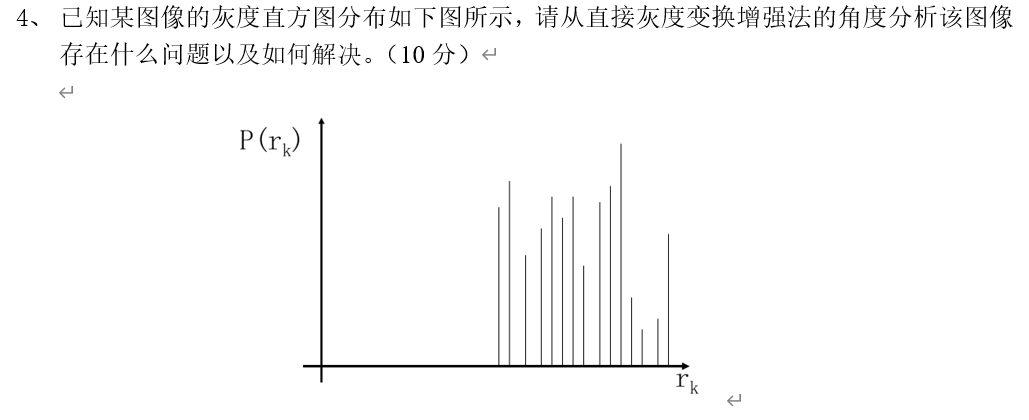
答：该图像存在较亮的问题，灰度直方图分布在较高的区域。从直接灰度变换增强法的角度，我们可以采用指数函数变换，对高灰度区进行扩展。

tip

分析：该图像中没有低灰度的像素，全部集中在高灰度部分，因此使用指数函数变换将原来的集中的高灰度区域进行拉伸，扩展其灰度分布的范围，从而起到增强效果。

直方图灰度变换

直方图均衡化

• 目的：

  将一非均匀灰度概率密度分布的图像，通过某种灰度变换，将其变成一幅具有均匀灰度概率密度分布的目的图像。

• 步骤：

  1. 根据原始图像计算原始灰度密度分布函数$r_k$

  2. 计算变换函数，即累积密度分布函数$s_k$

  3. 计算均衡化后的灰度级$s(k)$，即使用以下公式进行均衡化映射：

     $$s(k)=\mathbf{ceil}(s_k\times L-1)\tag{13}$$

     其中，$L$是原直方图中灰度级数。

  4. 画出最终均衡化后的直方图

例题：

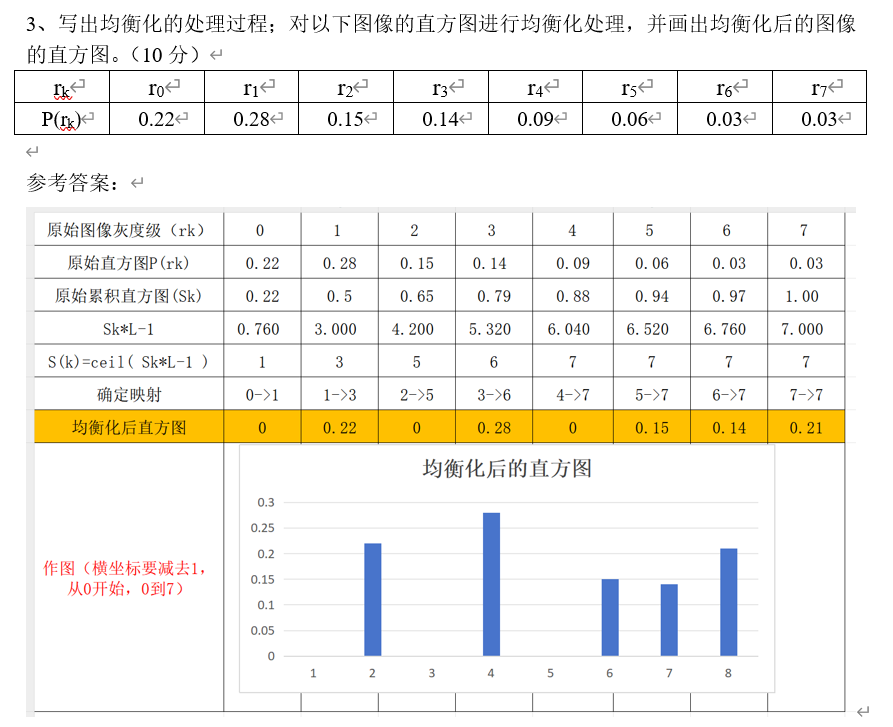
直方图规定化

• 目的：

  调整原始图像的直方图使其符合某一规定的直方图的要求。

• 思想：

  将原始图像和规定图像进行均衡化后，二者的灰度概率密度分布相同，进行对应映射即可。

• 步骤：

  1. 对原始图像进行均衡化，得到映射后的$s(k)$
  2. 对规定的图像直方图进行均衡化，得到映射后的$z(k)$
  3. 由于$s(k)$和$z(k)$都是归一化后的均匀分布，使用二者之间的就近原则将$s(k)$对应到给出的规定直方图的灰度级
  4. 画出规定化后的直方图

• 例题：

  

  

  

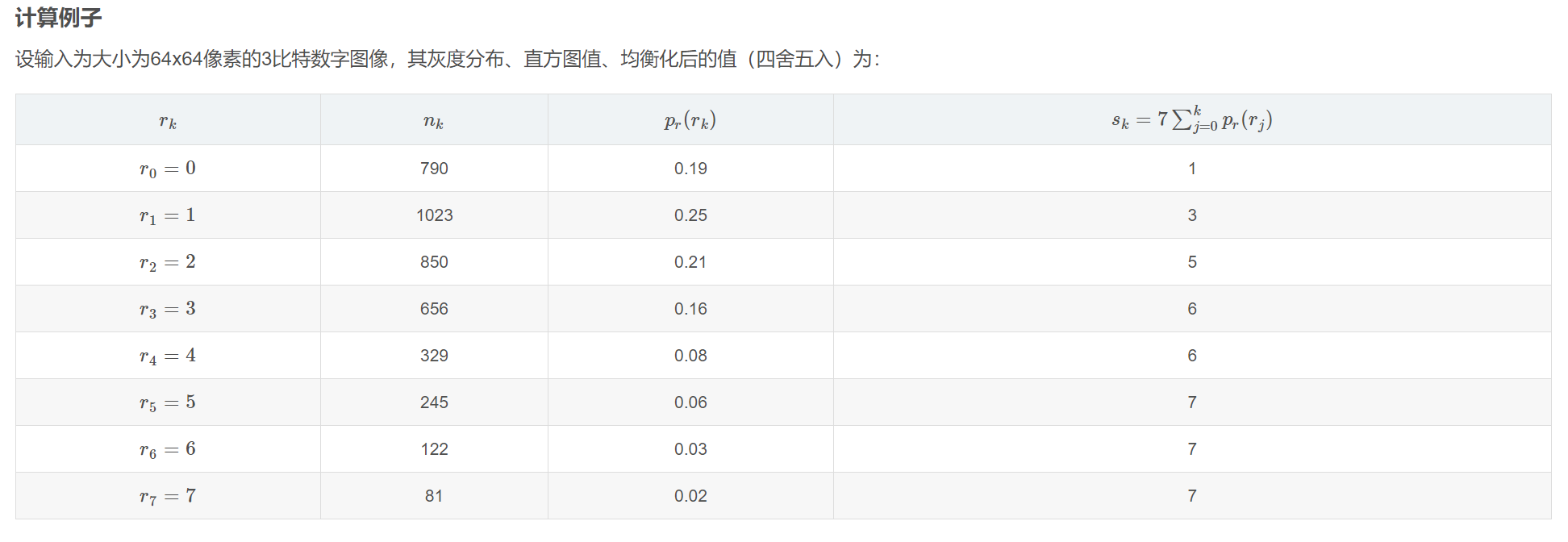
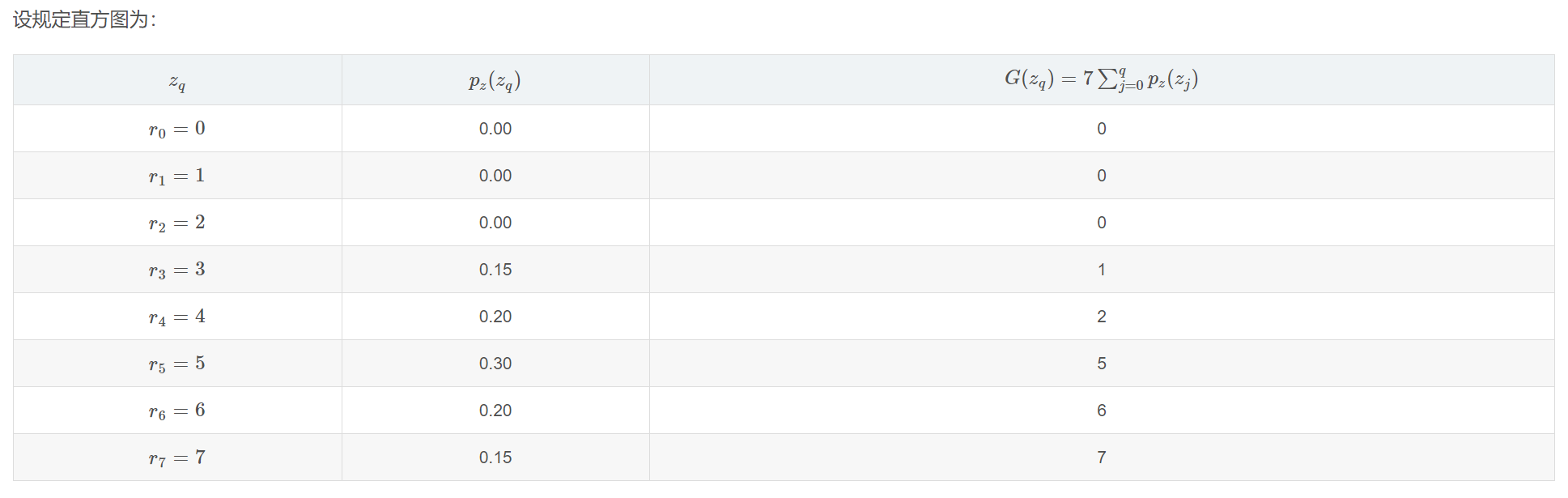
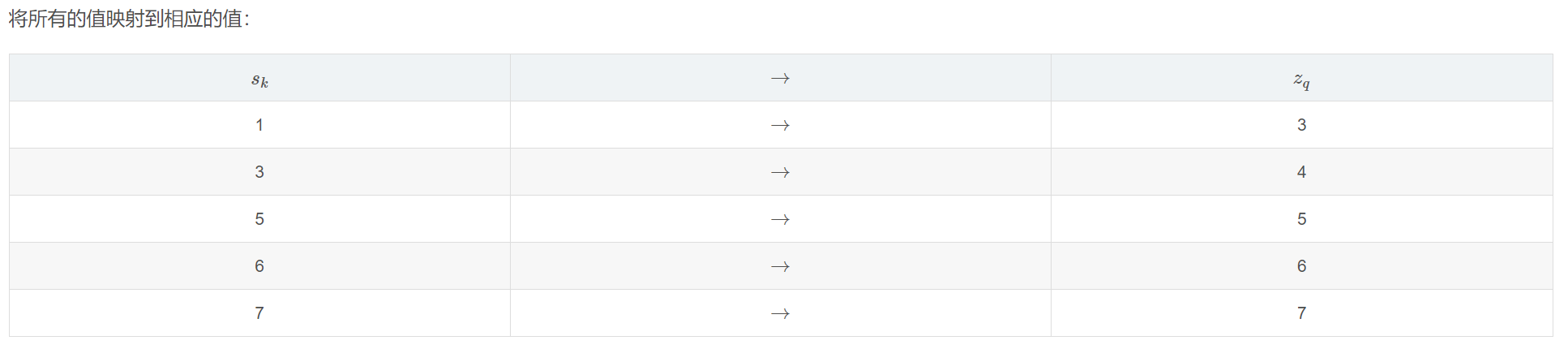
  此时已经获得了原始图像均衡化后的灰度级与目标规定化输出的图像的灰度级之间的映射关系，最后一步按照$r_k$画出目标规定化输出的图像直方图即可。

空域滤波增强

空域滤波可以根据作用分为平滑滤波以及锐化滤波。

平滑滤波

important

噪声的特点：

• 随机性
• 叠加性
• 噪声与图像之间具有相关性

线性平滑滤波

1. 邻域平均滤波
2. 加权平均滤波
3. 高斯滤波

非线性平滑滤波

1. 中值滤波
2. 最大值滤波
3. 最小值滤波

锐化滤波

锐化滤波消除或减弱图像的低频分量从而增强图像中物体的边缘轮廓信息，使得除边缘以外的像素点的灰度值趋向于零。

1. 梯度法
2. 拉普拉斯算子，非线性滤波
3. 定向滤波：检测特定方向边缘的滤波，通常在模板上表现为在该特定方向上模板值较大。

下面的表格展示了水平方向的定向锐化模板

-1	-1	-1
2	2	2
-1	-1	-1

下面的表格展示了对角方向的定向锐化模板

-1	2	-1
-1	2	-1
-1	2	-1

第6章 图像频域增强

图像从空域变换到频域后，低频分量对应图像中灰度值变化缓慢的区域，可能是图像的背景；高频分量表示图像中灰度值变化迅速的区域，可能是图像的噪声或物体的边缘。

在图像频谱（经过中心偏移的）中，中心代表低频信息，四周代表高频信息。

低通滤波

抑制、衰减高频分量，保留低频分量。

理想低通滤波器（ILPF）

tip

ILPF means Ideal Low Pass Filter.

$$H(u,v)=\begin{cases}1&D(u,v)\leq D_0\\ 0&D(u,v)>D_0\end{cases}\tag{14}$$ $$D(u,v)=\sqrt{u^2+v^2}\tag{15}$$

在截止频率$D_0$处垂直截止，通过频率和截止频率在$D_0$处具有不连续性，通带和阻带之间没有过渡，会产生无限的振铃效应。

巴特沃斯低通滤波器（BLPF）

通带与阻带之间过度平坦，通过频率和截止频率之间没有明显的不连续性，不会出现振铃效应。

$$H(u,v)=\frac{1}{1+(\sqrt{2}-1)[\frac{D(u,v)}{D_0}]^{2n}}\tag{16}$$

其中，取$H(u,v)$下降到最大值的0.707时的$D(u,v)$作为截止频率$D_0$。

即当$D(u,v)$达到截止频率时，$\frac{D(u,v)}{D_0}=1$，此时$H(u,v)=0.707$。

指数低通滤波器（ELPF）

一般情况下，取$H(u,v)$下降到最大值的1/2时的$D(u,v)$作为截止频率。

$$H(u,v)=e^{-[\frac{D(u,v)}{D_0}]^n}\tag{17}$$

截止频率和通过频率之间具有更光滑的过渡，没有振铃现象。且指数低通滤波器比巴特沃斯低通滤波器衰减更快，处理后的图像更模糊。

梯形低通滤波器（TLPF）

由于在$D_0$尾部包含高频分量$D_1$，处理后图像的清晰度较理想低通滤波器有所改善，但会出现振铃效应，

$$H(u,v)=\begin{cases}1&D(u,v)<D_0\\ \\ \frac{D(u,v)-D_1}{D_0-D_1}&D_0\leq D(u,v)\leq D_1\\ \\ 0&D(u,v)>D_1\end{cases}\tag{18}$$

高通滤波

抑制低频分量，保留高频分量。

理想高通滤波器（IHPF）

$$H(u,v)=\begin{cases}1&D(u,v)>D_0\\ 0&D(u,v)\leq D_0\end{cases}\tag{19}$$

性质与理想低通滤波器一样，垂直截断，具有无限振铃效应。

巴特沃斯高通滤波器（BHPF）

$$H(u,v)=\frac{1}{1+(\sqrt{2}-1)[\frac{D_0}{D(u,v)}]^{2n}}\tag{20}$$

通常采取$H(u,v)$下降到最大值的0.707时的$D(u,v)$作为截止频率，没有振铃效应。

指数高通滤波器（EHPF）

$$H(u,v)=e^{-[\frac{D_0}{D(u,v)}]^n}\tag{21}$$

梯形高通滤波器（THPF）

$$H(u,v)=\begin{cases}1&D(u,v)>D_0\\ \\ \frac{D(u,v)-D_1}{D_0-D_1}&D_1\leq D(u,v)\leq D_0\\ \\ 0&D(u,v)<D_1\end{cases}\tag{22}$$

带通和带阻滤波

带通滤波

顾名思义，带通滤波就是允许某一特定频率的信号通过，而衰减频率范围之外的信号。

理想带通滤波的传递函数为：

$$H(u,v)=\begin{cases}0&D(u,v)<D_0-\frac{w}{2}\\1&D_0-\frac{w}{2}\leq D(u,v)\leq D_0+\frac{w}{2}\\0&D(u,v)\geq D_0+\frac{w}{2}\end{cases}\tag{23}$$

其中，$D_0$是通带中心频率，$w$是通带宽度。

带阻滤波

顾名思义，带阻滤波就是衰减某一特定频率范围的信号，而允许频率范围之外的信号通过。

理想带阻滤波的传递函数为：

$$H(u,v)=\begin{cases}1&D(u,v)<w_1\\0&w_1\leqslant D(u,v)\leq w_2\\1&D(u,v)> w_2\end{cases}\tag{24}$$

第7章 彩色图像处理

伪彩色图像的处理

伪彩色图像的增强一般用于B超、石油开采以及安检方面。

全彩色图像的处理

第8章 图像复原

图像退化机理

退化原因

1. 成像系统镜头聚焦不准产生的散焦
2. 相机与景物之间的相对运动
3. 成像系统存在的各种非线性因素以及系统本身的性能
4. 模拟图像在数字化过程中，因数字化的精度和误差而损失图像细节
5. 成像系统中存在的各种随机噪声

复原机理

图像复原的过程一般是沿着图像退化的逆向过程进行的。首先根据先验知识分析退化原因，了解图像变质的原理，在此基础上建立图像的退化模型，然后以图像退化的逆过程对图像进行处理。

图像复原与图像增强的区别和联系

联系：二者从表面上看都是为了提高图像的质量。

区别：二者在目的和过程上都有明显的区别。

在目的上，图像增强是为了提高图像的视感质量，增强后的图像可能损失一些信息，并与原始图像有一定的差异；而图像复原是为了使待复原的图像与原始图像尽可能的接近。

在过程上。图像增强一般不考虑图像退化的真实过程，而是使用特定技术来突出和强调图像中所关注的特征；而图像复原是直接针对图像产生退化的原因建立相应的数学模型，并沿着退化的逆向进行复原。

图像退化模型

图像$f(x,y)$经过退化系统$H(x,y)$后再与噪声$n(x,y)$叠加，得到最后退化的图像$g(x,y)$。

退化系统的一般特性：

1. 线性特性。
2. 空间位置不变性：经过退化系统后的输出只有输入有关，而与输入在图像中的位置无关。

第11章 图像分割

阈值分割法

最佳阈值法

假设图像由物体和背景两部分组成，且物体像素的分布和背景像素的分布均符合正态分布，物体像素的正态分布概率密度函数的均值为$\mu$，背景像素的正态分布概率密度函数的均值为$\nu$，则最佳阈值法确定的阈值为

$$t=\frac{\mu +\nu}{2}\tag{25}$$

判别分析法

通过计算灰度直方图的0阶矩和1阶矩最大化类间方差从而得到最佳阈值。

边缘检测的基本原理

1. 什么是图像的边缘？

   图像中结构具有突变的地方，表明一个区域的终结，也是另一个区域的开始，这种不连续性称为边缘。

2. 边缘信号的类型？

   1. 阶跃型，但实际情况中不可能有完全理想的突变。突变处为边缘点。
   2. 渐变型，逐渐增大或逐渐减小。渐变的中间位置为边缘点。
   3. 台阶型。台阶的中间为边缘点或认为台阶两侧为两个边缘点。

边缘检测算子

Robert算子

• 一阶导数算子。
• 利用局部差分方法，采用对角线方向相邻两像素之差近似梯度幅值检测边缘。
• 对噪声敏感，不能抑制噪声。

Sobel算子

• 一阶导数算子。
• 先进行加权平均，然后进行微分运算。
• 对噪声具有一定的抑制能力。

Prewitt算子

• 一阶导数算子。
• 利用局部差分平均方法寻找边缘。两个模板一个检测水平边缘，一个检测竖直边缘。
• 对噪声具有一定的抑制能力。

Laplace算子

• 二阶导数算子。
• 使噪声成分得到加强，对噪声更敏感。
• 与Marr边缘检测算子一样，一般先进行低通滤波平滑后再进行二阶微分运算。

Canny边缘检测

1. 使用高斯滤波平滑图像
2. 计算梯度幅值和方向
3. NMS非极大值抑制，保留每个像素点上梯度强度的极大值，删掉其他值
4. 使用双阈值方法确定强边界和弱边界
5. 滞后边界跟踪

课后习题中的问答题

1. 傅里叶频谱图的特征：

   • 频率分布：傅里叶频谱图展示了图像在不同频率下的强度分布。高频部分对应图像中的边缘和细节，低频部分对应图像中的整体结构和大致轮廓。
   • 能量分布：图像中不同频率的能量在频谱图中以不同强度的幅度呈现。高幅度的频率分量通常标示着图像中强烈的变化或边缘。
   • 平移不变性：傅里叶变换具有平移不变性，这意味着在频域中图像的平移对应于幅度谱中相位的改变而不影响幅度谱本身。

2. 如何在频域实现图像平滑

   1. 利用傅里叶变换将图像从空域转换为频域；
   2. 将频域图像进行中心偏移，使得低频信息在频谱中央；
   3. 利用滤波函数生成一个与图像大小相同的二维频域矩阵；
   4. 将图像的频域与滤波器的频域相应相乘；
   5. 将相乘后的频域再次逆平移到频域的原始位置；
   6. 将得到的频域进行逆傅里叶变换，得到滤波后的空域图像。

3. 一阶边缘检测算子与Laplace算子的异同。

   • 相同点：都可以检测边缘并且对噪声敏感
   • 不同点：一阶边缘检测算子检测到的边缘都有明确的方向，而Laplace算子对各种方向的边缘都有较好的响应

4. 已知一幅图像受到加性随机噪声污染，分析并写出三种去除或降低噪声的方法。

   空域滤波（均值滤波、中值滤波），频域滤波（巴特沃斯低通滤波），图像恢复技术。

5. 分析采样和量化的过程，以及它们对数字化图像质量的影响。

   采样是把空间上连续的图像转换为离散的抽样点，即像素。量化将抽样后所得的连续的像素值离散化为整数值。

   对数字化图像质量的影响：

   采样间隔越大，所得图像像素数越少，图像空间分辨率越低，质量越差。反之图像质量好，但数据量大。

   量化等级越多（灰度级数越多），所得图像层次越丰富，灰度分辨率越高，质量越好，但数据量大。反之，图像质量差，会出现假轮廓现象，但数据量小。

6. 图像噪声的特点。

   • 随机性
   • 叠加性
   • 噪声与图像之间具有相关性

7. 什么是线性灰度拉伸？线性灰度拉伸可以分为几种情况？

   线性灰度拉伸是将输入图像的灰度值的动态范围按线性关系拉伸扩展至指定范围或灰度的整个动态范围。

   线性拉伸可分为按比例线性拉伸和分段线性拉伸两种方法。同时，按比例线性拉伸又可以分为均匀线性拉伸以及限幅线性拉伸。

8. 伪彩色图像处理可以应用在哪些方面？

   • B超
   • 石油开采
   • 安检