数据结构

树

1. 树的性质：

   • 一棵 N 个结点的树有 N-1 条边
   • 树的总度数+1=树的结点数
   • 树的度=树中度最大结点的度数

2. 二叉树的性质：

   • 叶子结点数等于度为 2 的结点数加 1，即n0 = n2 + 1

     

3. 树转化为二叉树：

   参考资料：知乎

   1. **加线。**在所有的兄弟结点之间加一条线。
   2. 去线。树中的每个结点，只保留它与第一个孩子结点的连线，删除其他孩子结点之间的连线。
   3. 调整。每个结点的原来的孩子是结点的左孩子，由原来的兄弟结点转过来的孩子是结点的右孩子。

4. 二叉排序树：每个结点的左子树上的所有结点值都更小，每个结点的右子树上的所有结点的值都更大。

5. 平衡二叉排序树：要么是空树，要么左子树的高度与右子树的高度之差小于等于1。

图

1. 图的表示：

   • 邻接矩阵

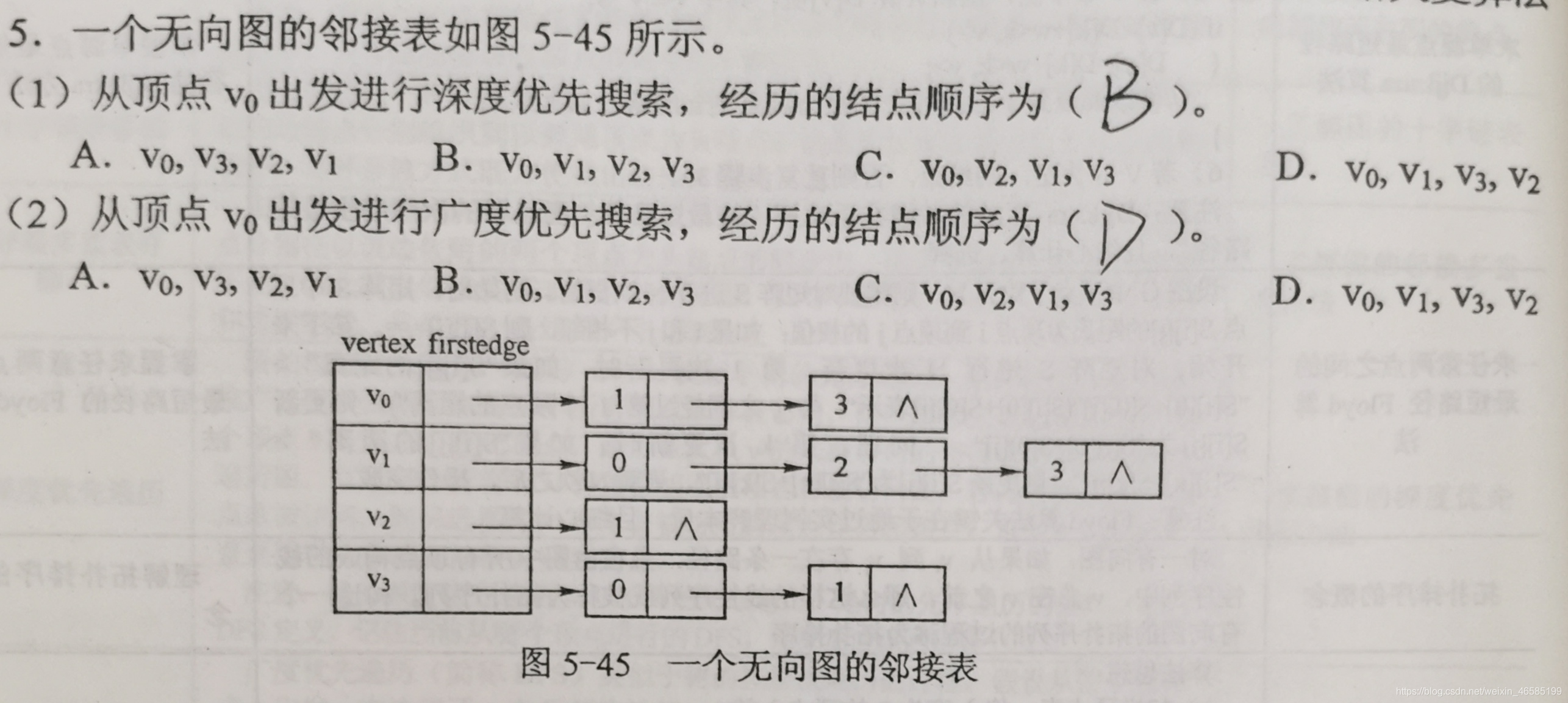
   • 邻接表**：每一行表示的是一个顶点所连接的顶点，链表不具有指向性**

     邻接表的搜索

     

2. 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

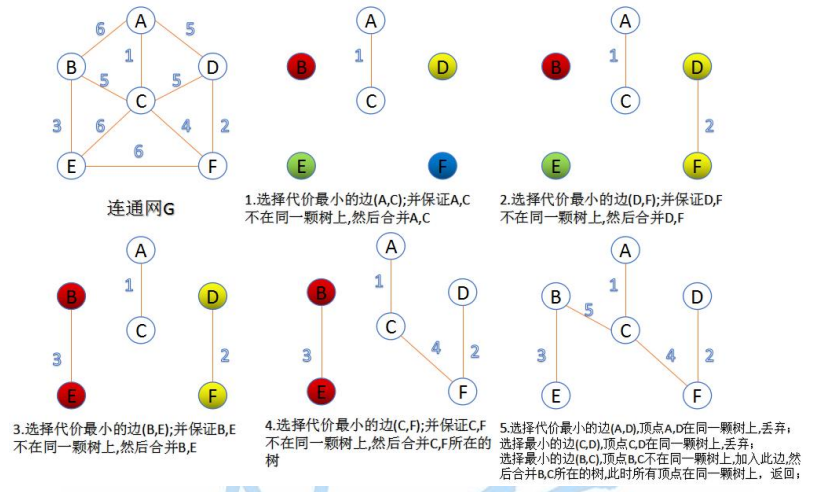
   • Kruskal算法

     

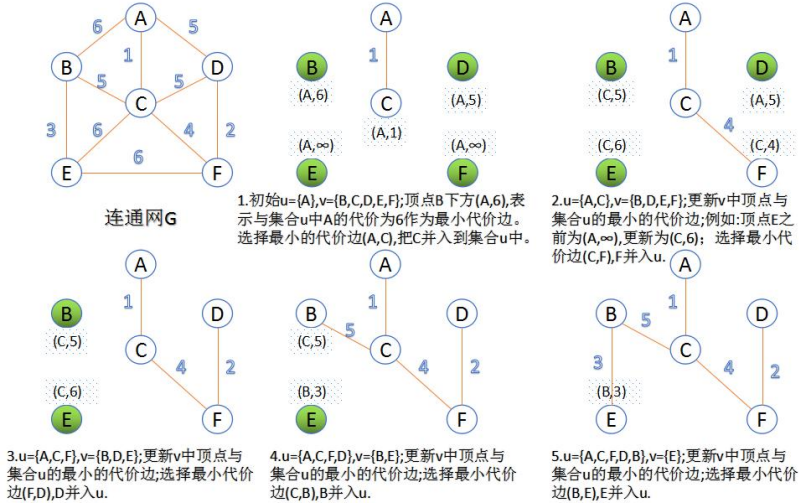
   • Prim算法

     

3. 最短路径

​

​